Boyer-Moore voting in Scade One: unlock the power of streaming algorithms

August 21, 2024 at 8:36 am

Solution

Participant

In software development, algorithms are the building blocks for efficient and robust applications. Among the popular algorithms, the Boyer-Moore Majority Algorithm stands out as a versatile solution for effectively and elegantly addressing a common problem: identifying the most frequently occurring element in a data set.

In this blog post, we will embark on discovering the mysteries of the Boyer-Moore Majority Algorithm and how this streaming algorithm can be efficiently implemented for critical embedded systems, building on Ansys Scade One benefits.

First, we will delve into the core functionalities of the algorithm by providing a clear explanation and visualizing the different steps. Next, we will go through implementing this powerful algorithm using Scade One, showcasing how the features of its modeling language (Swan) suit streaming algorithms. Lasty, we will highlight a few practical applications to demonstrate the key role of this algorithm.

So, let’s get started on our journey.

Algorithm Explanation

To begin our exploration, let us first understand the underlying problem we aim to address. Consider a sequence consisting of N distinct votes, each representing an element of a given type. Our objective is to identify if there exists a particular value appearing strictly more than half (>N/2) of the total votes in the sequence. If such a majority value exists, our task is to convey this information to the user.

For illustrative purpose, let’s examine two examples:

For [3, 1, 1, 4, 1] of length 5, we would obtain the value 1 as it is present 3 times.
For [3, 1, 4, 1, 5, 9, 2, 6, 5] of length 9, we would have no majority as each value is only present 1 or 2 times.

Boyer-Moore algorithm vs alternative solutions

Some common algorithms for this problem are the following:

Algorithm	Time Complexity	Space Complexity
Brute Force: looping through each element and counting occurrence in the rest of the sequence	O(n²) nested loops	O(1) 2 variables
Hash table: count number of occurrence for each element	O(n) 2 iterations	O(n) frequency of each number
Boyer-Moore Majority Algorithm	O(n) 2 iterations	O(1) 2 variables

The Boyer-Moore Majority Algorithm proposed in the 80’s solves the issue at hand with a constant amount of memory (i.e., independent of the number of votes) and a linear time complexity. It does so by using only 2 variables that are updated when streaming through the sequence of votes: a candidate for the most frequent element m and a counter c.

A second iteration is then required to check whether the candidate is indeed present as majority by counting the number of occurrences and comparing to N/2.

The Boyer-Moore Majority Algorithm is a good example of a streaming algorithm: an algorithm for processing data streams in which the input is presented as a sequence of items examined in very few passes (usually one or two) with the advantage of operating with limited memory, making this type of algorithm ideal for embedded systems.

Pseudo-code and visualization of principle

The pseudo-code (for the first iteration) is the following, as found in Wikipedia:

Initialize an element m and a counter c with c = 0
For each element x of the input sequence:
- If c = 0, then assign m = x and c = 1
- else if m = x, then assign c = c + 1
- else assign c = c − 1
Return m

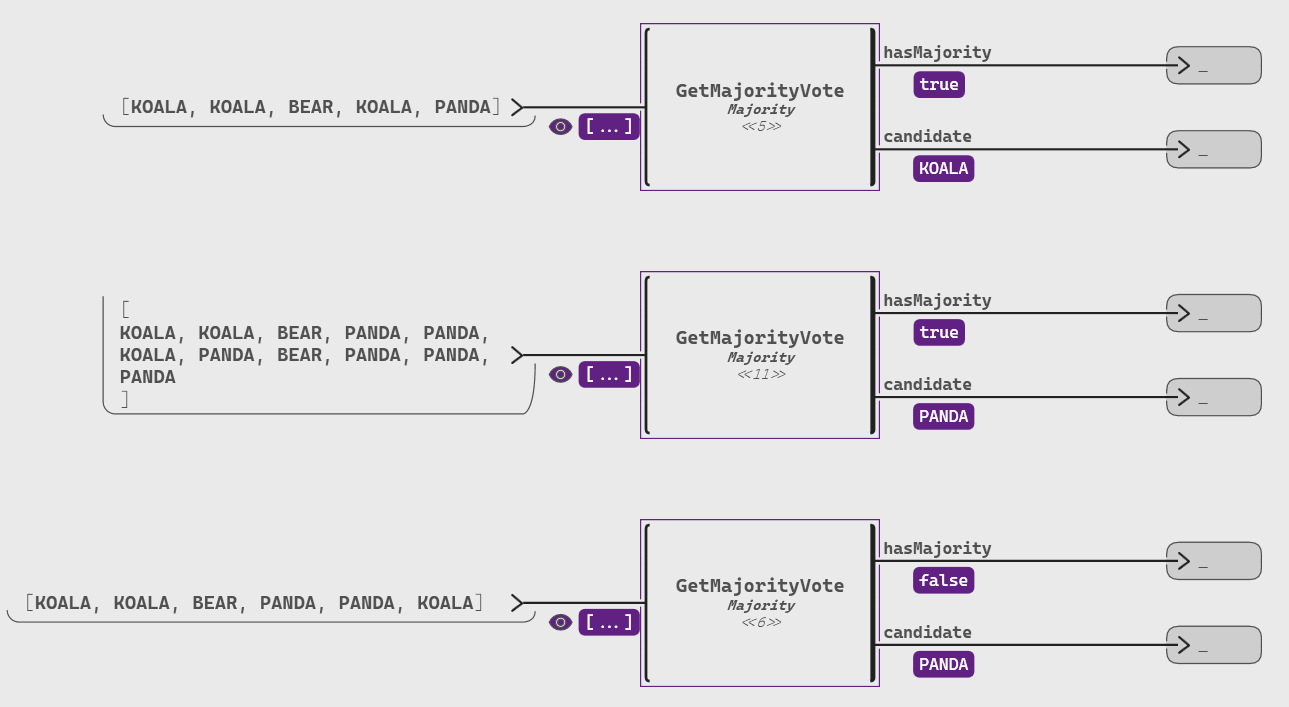
The following two examples showcase how the variables c and m help to determine the candidate for the majority (i.e., the last value of m).

With 3 koalas among the 5 votes, the candidate is the koala🐨:

Sequence	–	🐨	🐨	🐻	🐨	🐼
c	0	1	2	1	2	1
m	?	🐨	🐨	🐨	🐨	🐨

With 6 pandas among the 11 votes, the candidate is the panda🐼:

Sequence

–

🐨

🐻

🐼

🐨

🐼

🐻

🐼

🐨

🐼

It is important to note that this algorithm only detects strict majority: if we have an element that is present N/2 times or if we don’t have any majority at all, the returned candidate is arbitrary.

To illustrate this, in the following sequence of 6 votes containing 3 koalas (i.e., a non-strict majority of N/2), 2 pandas, and 1 bear, the algorithm would return the panda🐼 as the candidate instead of a koala🐨:

Sequence	–	🐨	🐨	🐻	🐼	🐼	🐨
c	0	1	2	1	0	1	0
m	?	🐨	🐨	🐨	🐨	🐼	🐼

Implementation of Boyer-Moore Majority Algorithm in Swan

This streaming algorithm is favorable to critical embedded systems, and Swan (the Core Language of Scade One) is a good match for implementing it:

The sequential treatment of the input values (i.e. votes processed in the array order) ensures a predictable execution path: this aligns perfectly with Swan’s data-flow programming model
The constant memory usage ensures predictable resource allocation and maintains system stability: Swan is designed to use constant memory in the design of software applications in embedded systems with limited resources

For our implementation we assume that we have an input array of N votes with at least one vote. We want to compute both the candidate and whether this candidate represents a strict majority among the votes.

The implementation in Swan is done in these steps:

Implementation of a “vote counter” to compute the values of c and m at each step
An iteration of this counter on the sequence of votes to get the candidate
A second iteration on the sequence of votes to count the number of occurrences of the candidate and then a comparison is done with N/2 to assess whether it is a strict majority

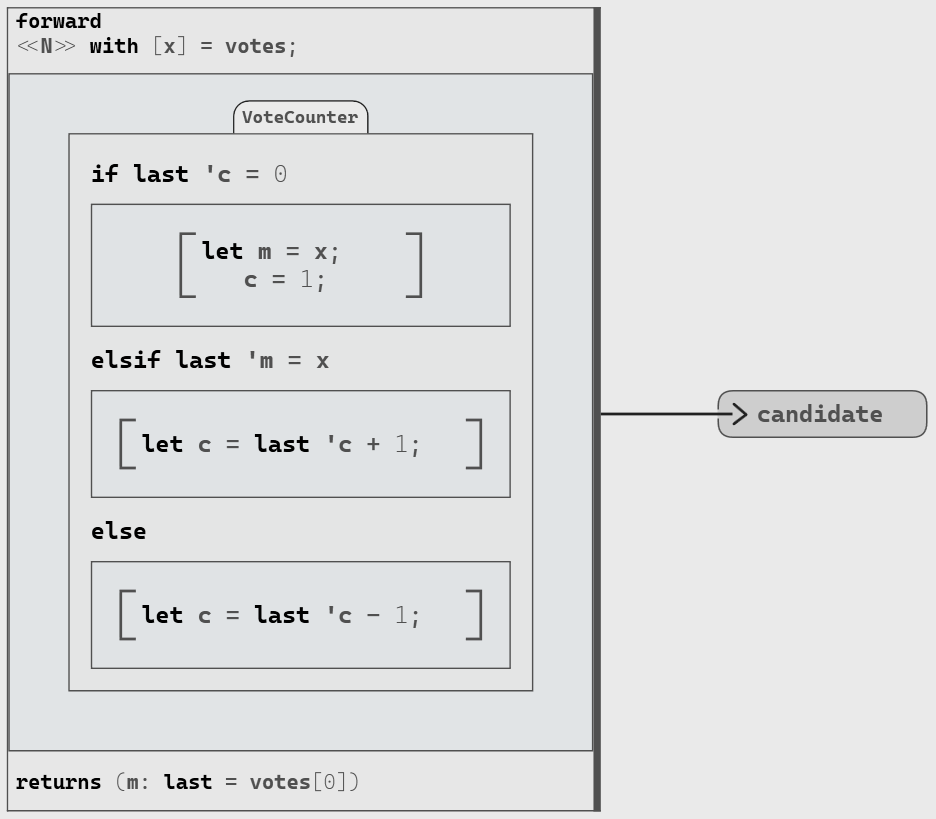
The “vote counter” corresponds to the following part of the pseudo-code:

If c = 0, then assign m = x and c = 1
else if m = x, then assign c = c + 1
else assign c = c – 1

We can implement this with an “Activate If” block that will activate a part of our model based on given conditions: we will perform the different assignments based on the conditions above.

As Swan is a data-flow language with sequential logic, the definition in a flow cannot depend on itself. Therefore, when incrementing / decrementing the variable c, we need to use the keyword last 'c, which allows us to reference the value of c from the previous iteration. The same applies when checking the condition c = 0.

Computing the candidate

For the iteration to compute the candidate, we shall use the “forward” operator of Swan: a loop-like construct allowing to iterate a computation on a finite flow provided by an array (see this blog post for an introduction).

For the forward operator, we need to specify that:

We iterate over all the N votes, and we access each vote with the variable x: this corresponds in Swan to the notation <‍‍> with [x] = votes;
The output of this iteration is the candidate m, with a default (initial) value set to the first vote: we write it in Swan with the notation m: default = votes[0]
The variable c (an integer) of the “vote counter” is a local variable for which we need the previous value, and the first value is 0: we write it in Swan with the notation c: int32 last = 0
The body of the forward is the vote counter we just described

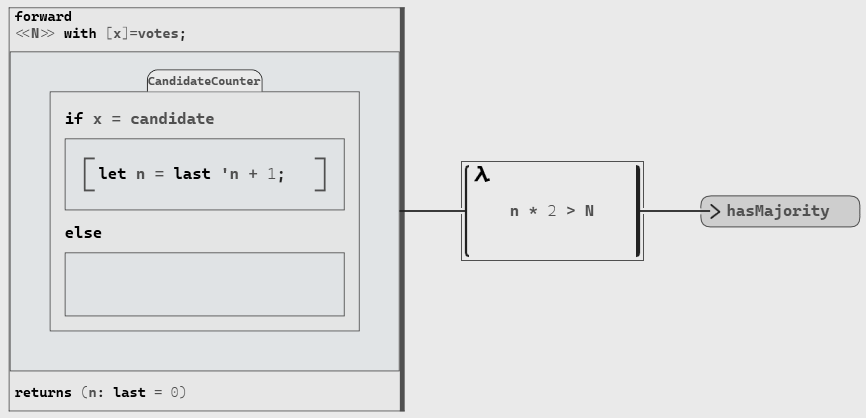
The next step is to count the number of occurrences of this candidate in the votes. To do so, we can use a forward block and specify that the initial value of our counter is 0 with notation n: last = 0.

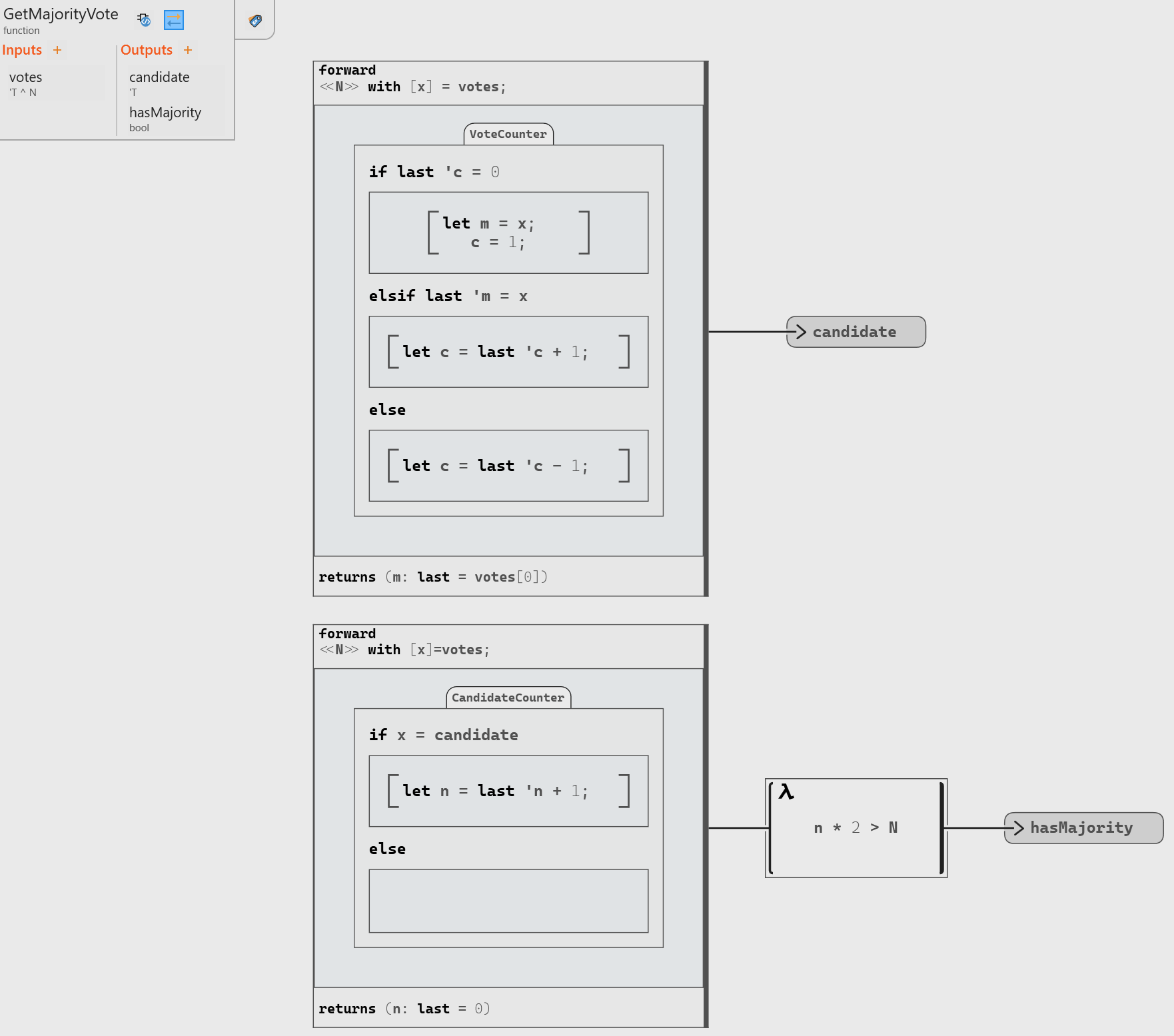
We can then check whether this strictly more than half of the number of votes. To avoid rounding errors during integer divisions (e.g. 5 / 2 = 2), we will compare N and the double of the number of occurrences. One simple way is to use an anonymous operator that we implement with: function n =‍> n * 2 ‍> N.

The final model to compute both the candidate and whether we have a strict majority will look like the diagram below (with the votes being of a polymorphic type 'T that could be any value).

Usage of Boyer-Moore Majority Algorithm

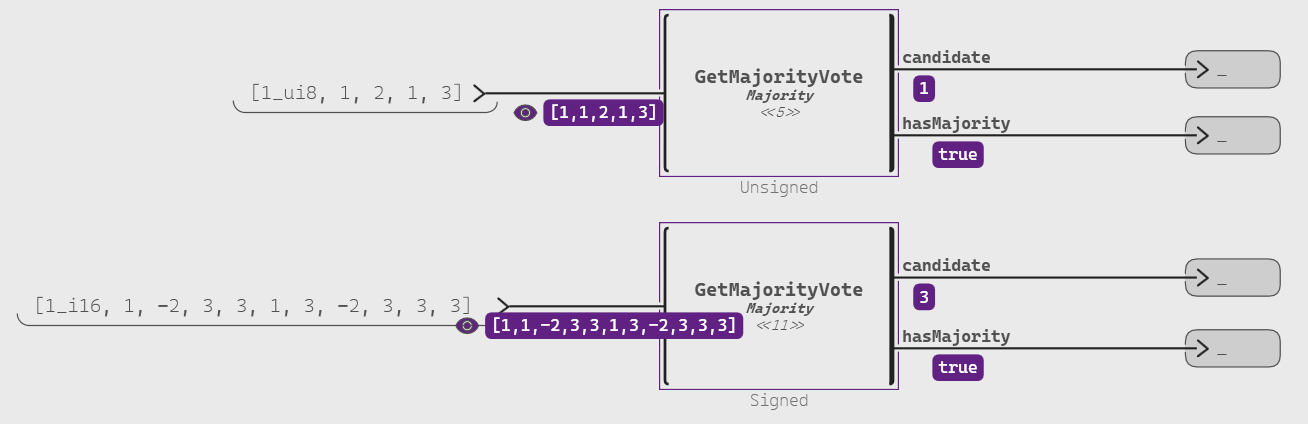
The algorithm’s reliance on a simple equality comparison offers great adaptability, as it can accommodate any data type for which the = operator (i.e. equality) is defined. This flexibility allows the algorithm to be highly versatile in different application scenarios.

Therefore, by using a polymorphic type for the input of our model, we can use any such data in our Scade One implementation (e.g. unsigned integers, signed integers, or enumerates):

The versatility of the algorithm and its streaming nature makes it suitable for a wide range of applications in safety-critical embedded systems:

Fault-Tolerance in Sensor Data Fusion: when using multiple sensors, if one or more sensors produce incorrect data due to malfunction or noise, we can determine the most probable accurate value by calculating the majority reading
Data Consolidation in Consensus Algorithms: the algorithm can combine data from various sources (e.g. sensors like cameras, radar, and LIDAR when used in Driver Assistance Systems) allowing an accurate and reliable decision-making based on the consolidated information
Anomaly Detection in Real-Time Monitoring Systems: in systems that receive continuous data inputs, the algorithm can be used to detect anomalies or deviations from normal patterns, which could be a sign of potential system failure or threat

Note that when dealing with voting amongst redundant sensors streaming floating-point values, it is advisable to choose an algorithm based on their order rather than a majority vote system, such as the median. This approach provides accurate and reliable results.

Explore Further

Download the example in this blog here. If you are a SCADE user, access Scade One Essential with your existing licenses on the Ansys Download Portal and experiment with this example!

This blog showcases the invaluable role of Boyer-Moore Majority Algorithm for software engineers specializing in embedded systems and how the new forward construct of Scade One makes the implementation of this streaming algorithm easy and efficient. Learn more about the forward block by visiting the “Language Explanations” section of Scade One User Documentation.

Schedule a live demo of Scade One using this link.

About the author

Jean-François Thuong (LinkedIn) is a Software Validation Manager at Ansys. He excels in software development, testing, and team management. His areas of expertise include the SCADE product, with a particular focus on Scade One. He is fluent in French, English and Chinese.