Free Courses Fluids Structures Electronics 3D Design Optics Photonics Materials Installation Python Optimization Safety & Cybersecurity Embedded Software MBSE Digital Mission Engineering STEM NVH Student Teams Indo Kursus Partner Courses My Courses

[Solution]

Introduction

In a previous blog series, we have introduced Swan, the domain-specific language used for modeling in Scade One. In this new blog, we want to illustrate a new construct available in Swan, using examples, and show typical use cases. We will look at array and matrix operators using the forward block, a new loop-like construct for iterative algorithms.

Scade One’s new forward block

About matrices in Swan

Before we get started, let’s recall a few things about matrices in Swan. Matrices are represented as arrays of arrays. A : T^M^N means that A is an array of size N where each cell is an array of size M. It represents a matrix of N rows by M columns.

The element a_ij (the element at row i and column j) in A of type T^M^N is accessed with syntax A[i][j], with 0≤i

For example, let’s consider the following matrix:

Its Swan type is int32^5^3: an array of size 3 where each element is an array of size 5: [[1,2,3,4,5], [2,1,4,1,3], [2,2,3,2,2]].

Introducing the forward block

A first example: the dot product

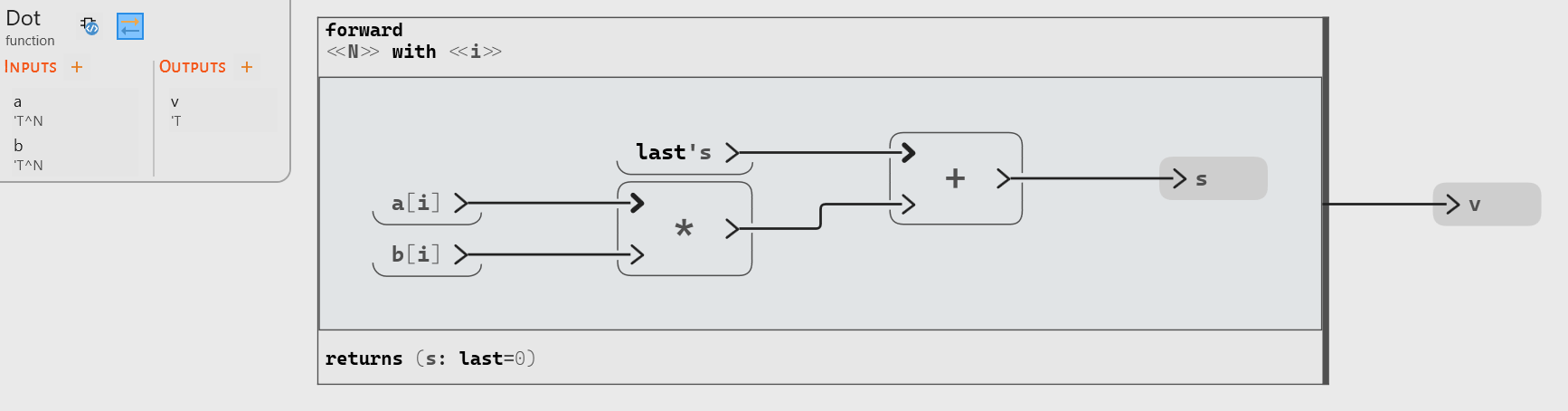
Our first example to introduce the forward is a usual operation on vectors: the dot (or scalar) product. It is defined as:

Here is the Swan version:

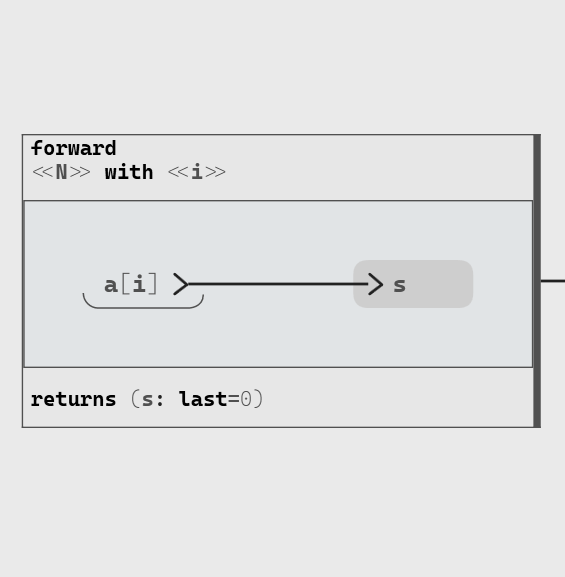
The Dot operator takes as input two arrays a and b of size N and base type ‘T and returns v of type ‘T. Note that this operator is generic (or polymorphic): it can be used for any value of N and any numeric type ‘T.

The body of the operator contains a forward block, that is made of:

• At the top, the declaration of the size of the iteration (N) and the name of the iteration index (i);
• At the bottom, the declaration of the output s, initialized to 0;
• The body of the operator that defines the value of s for each iteration;

But what does it mean? Remember that in Swan, operations are performed on sequences of values called flows. The idea of the forward is to see arrays as finite sequences and apply Swan operators on them, as illustrated below:

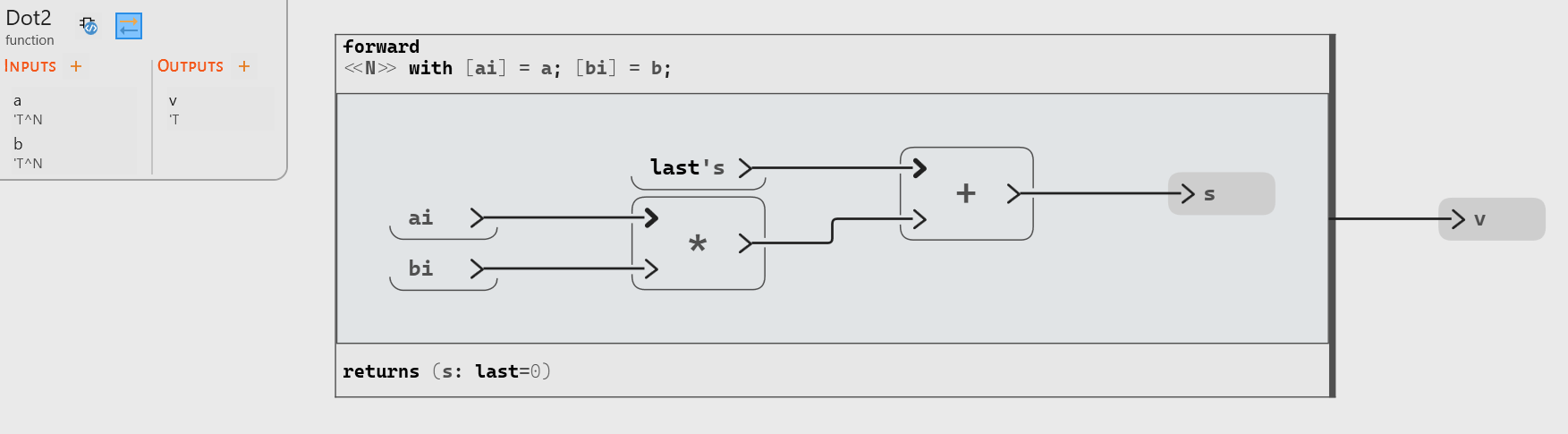
In this example, the value of s is obtained by adding the value of a[i] * b[i] to last's, which corresponds to the value of s during the previous iteration (and to the initial value 0 for the first iteration). The forward block returns the value of s during the last iteration, which is indeed the value expected for the dot product.

Note that it is also possible to declare input flows for the forward block, to directly iterate on one or several input arrays. Here is the same operator using this alternative approach:

[ai] = a declares a local flow ai representing the current element of the iterated array inside the forward.

Building arrays with a forward

A forward block can also be used to build a new array. Let us look at an example of this, with an operator that returns the diagonal vector of a matrix:

The input of GetDiagonal is a matrix of size N by N and the output is an array of size N. In order to declare an array, brackets are put around the declaration of the output: [vi]. It means that the output of the forward block is the array of successive values of vi.

At this point, you might think that the forward block is just like an imperative for loop. But this is not the case. Notice for example that each element of the output array is only defined once. The addition of the construct does not break the safe usage of arrays in Swan: arrays have a static size, no out-of-bounds accesses, arrays are fully defined.

Using the forward block for matrix computations

Matrix multiplication

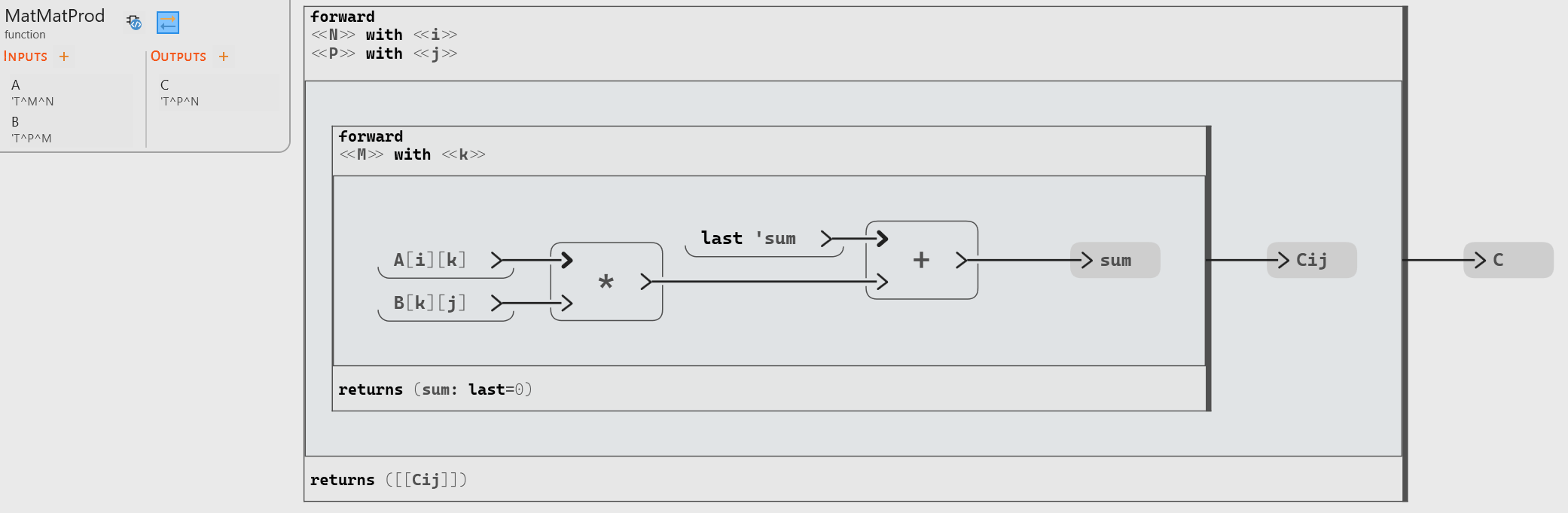
Now let us look at a couple more examples to highlights some of the benefits of the forward, starting with the matrix multiplication:

The implementation with a forward has many benefits, it particular compared to the usage of iterators as available in Scade 6 (see next section):

• The first thing to notice is that this implementation of the matrix multiplication is close to the usual specification for this algorithm, with three nested loops:

Matrix multiplication algorithm (from Wikipedia)

• The whole algorithm is defined in a single operator. There is no need to define an operator to be iterated.
• Inside the forward, static array projection can be used directly (here A[i][k] and B[k][j]), as long as the index used can be shown to be within the bounds of the array. There is no need to transpose arrays to put them in the correct shape for iterating.

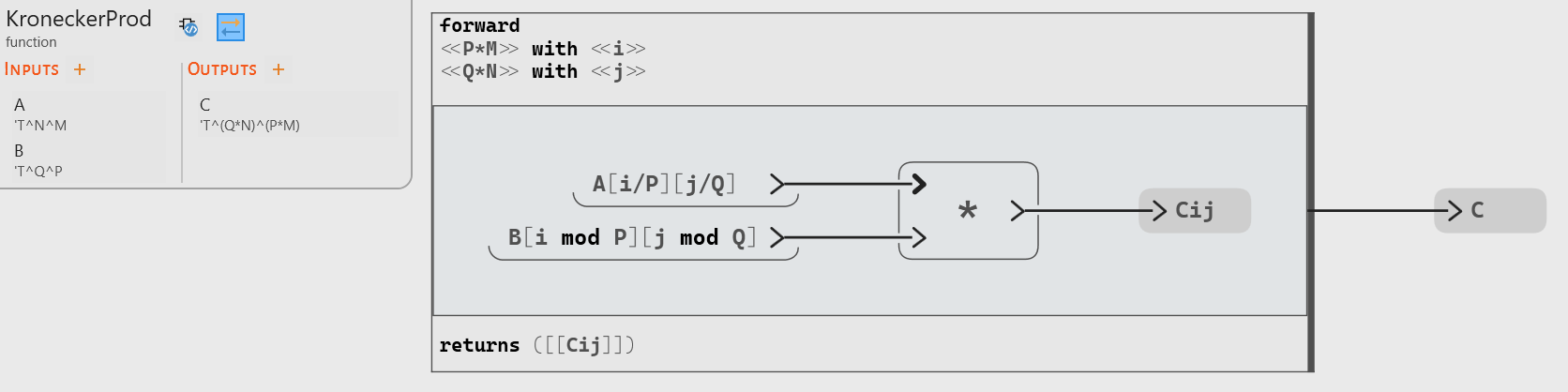
Kronecker product

The Kronecker product, sometimes denoted ⊗, is a special case of the tensor product, defined as:

If A is an m by n matrix and B is a p by q matrix, then the Kronecker product A ⊗ B is a pm by qn matrix that can be computed by:

where // is the integer division and % the remainder.

Here is the Swan implementation of this operation:

Again, this is a straightforward implementation in Swan of the formula shown above. What is interesting here is that this is not an iteration on the input matrices, but an iterative algorithm that defines the elements of the output matrix.

The various examples shown here demonstrate that Swan is not just about assembling predefined blocks. You can program more complex operations, to create generic, reusable libraries. But don’t worry, you don’t have to start from scratch. Scade One includes a standard library of Swan operators, including all the operators shown here (that will be available in 2025 R1).

What about iterators?

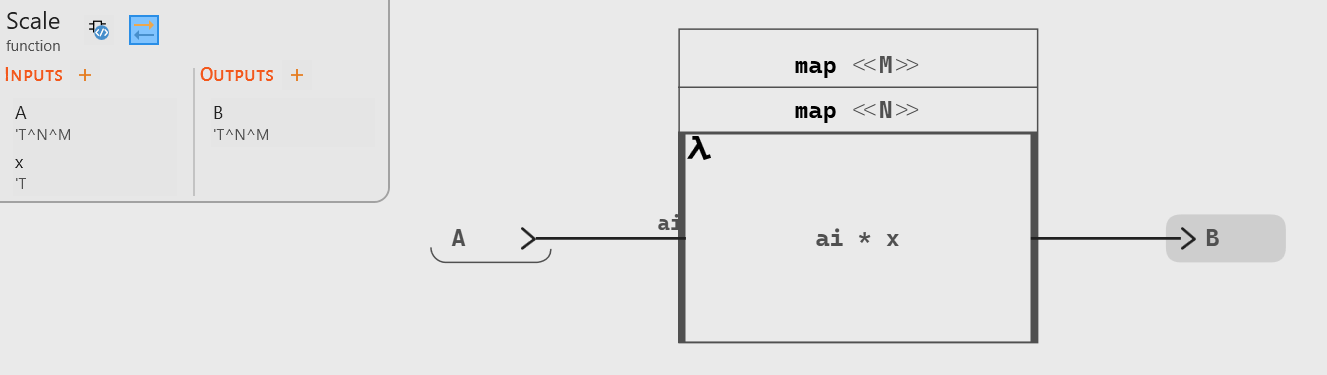
If you are a SCADE user, you are probably wondering about iterators in Swan. As we have shown here, the forward construct allows to create simpler, easier to understand implementations. But Swan still includes basic iterators (map[i], fold[i] and mapfold[i]) that can be used for instance for simple iterations, like multiplying all the elements of a matrix by a scalar:

Iterators have also received some love and improvements in Swan:

• Iterators can be nested, allowing to easily iterate on a matrix, as shown in the example above.
• The iterated operator is here an anonymous operator (similar to a lambda function in other programming languages), which means that there is no need for a separate operator declaration.

Want to learn more?

You can download the examples from this blog here. Remember that if you are a SCADE user, you can access Scade One Essential with your existing licenses. Just go the Ansys Download Portal and start experimenting!

This blog has given you a glimpse of the new forward construct. If you want to learn more about the forward block, you can look at the ‘Language explanations’ section of Scade One user documentation, that goes in more details. In future blogs, we’ll show more use cases of the forward block for manipulating other data structures.

Also, if you’d like to schedule a live demo of Scade One, you may do so by following this link.

About the author

Cédric Pasteur (LinkedIn) is a Senior Product Manager at Ansys. He has been working on Scade One, Ansys’ latest-generation model-based embedded software development product, since its inception. He specializes in programming language theory and its application to safe embedded systems.