Free Courses

[Solution]

Introduction

In a previous blog series, we introduced Swan, the domain-specific language designed for modeling in Scade One. We also explored how the forward block facilitates the implementation of array and matrix operators with a new loop-like construct for iterative algorithms.

In this new blog, we will showcase the pack operator, a powerful new construct available in Swan, that helps address common uses cases in signal processing such as correlation, convolution, cross-correlation, and more.

The problem space

In today’s article, we will demonstrate how to to solve a signal processing problem with Scade One: detecting shapes in a noisy 2D image. To achieve this, we will implement a (somewhat naive) Scade One cross-correlation algorithm that demonstrates core principles.

The solutions presented in this article can apply to any signal processing problem that looks at a signal’s current value and its neighbors. This includes many common applications: filtering, edge detection, blurring, sharpening, correlation, convolution, etc.

A note on safe array access in Swan

One way to implement our algorithm would be to process our signal using a fixed-size, sliding window of elements.

By construction, the Swan language enables safe usage of arrays: arrays have a static size, no out-of-bounds accesses, and are fully defined. Any time we need to dynamically access an array index, we benefit from Scade One’s native array access protection. It returns a default value if the index is not within the array’s bounds:

In some cases, the model designer may have already added a similar protection to the index computation itself. Such an approach may introduce uncoverable points in the model, that may later need to be justified during validation.

One thing to note is that the above construct introduces an if statement in the generated C code. Signal processing algorithms often involve processing large arrays and reading several contiguous values. Relying on the above construct for such a large number of reads would be detrimental to performance; we are therefore going to rely on another construct that fits our purpose better.

Introducing the pack block

In the Swan language, successor of Scade, the new pack block allows us to process a Swan array or matrix by chunks, which may or may not overlap.

The pack operator guarantees safe and efficient usage of arrays without the need to specify redundant default values.

Swan language reference

pack<‍<‍k,m‍>‍>(A) returns the array composed of m chunks of size k; chunks can overlap. If A is of size n, B = pack<‍<‍k,m‍>‍>(A) is such that B[i][j] = A[s*i*j] where s = (n-k)/(m-1) input: an array of type T^n input parameters: k, m two sizes verifying the conditions: m‍>1 and k<‍n and (m-1) divides (n-k) output: an array of type T^k^m

Examples:

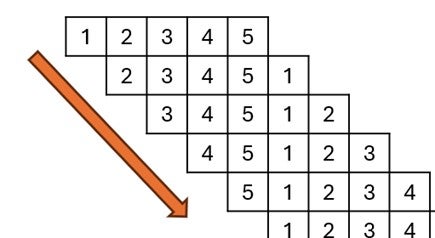
Let’s have a look at four use cases, starting from this stream of values:

We want to apply an iterative algorithm on:

• 4 chunks with size 5 without overlap between each chunk.

n = 20, size of the stream k = 5, size of each chunk s = 5, to avoid overlap Let’s verify constraints: s = (n - k) / (m - 1) or : m = (n - k) / s + 1 pack<‍<‍5 , (20 - 5) / 4 + 1‍>‍> pack<‍<‍5,4‍>‍> pack<‍<‍5,4‍>‍>(A) reshapes A from integer^20 to integer^5^4

• Overlapping chunks with size 5, shifted by 1.

n = 20, size of the stream k = 5, size of each chunk s = 1 Let’s verify constraints: s = (n - k) / (m - 1) or : m = (n - k) / s + 1 pack<‍<‍5 , (20 - 5) / 1 + 1‍>‍> pack<‍<‍5,16‍>‍> pack<‍<‍5,16‍>‍>(A) reshapes A from integer^20 to integer^5^16

• Overlapping chunks with size 5, shifted by 2.

n = 20, the size of the stream k = 5, the size of chunk s = 2 Let’s verify constraint: s = (n - k) / (m - 1) or : m = (n - k) / s + 1 The result has no integer solution: (m-1) does not divide (n-k). We need to add or crop values to or from the input stream to shift by 2 with pack pack<‍<‍5,9‍>‍>(A @ [A[19]]) reshapes A from integer^21 to integer^5^9

Using pack in one dimension

A common signal processing need is to apply an operation, such as ⊗, ⊕, *, or any user algorithm between a sliding mask and a stream values:

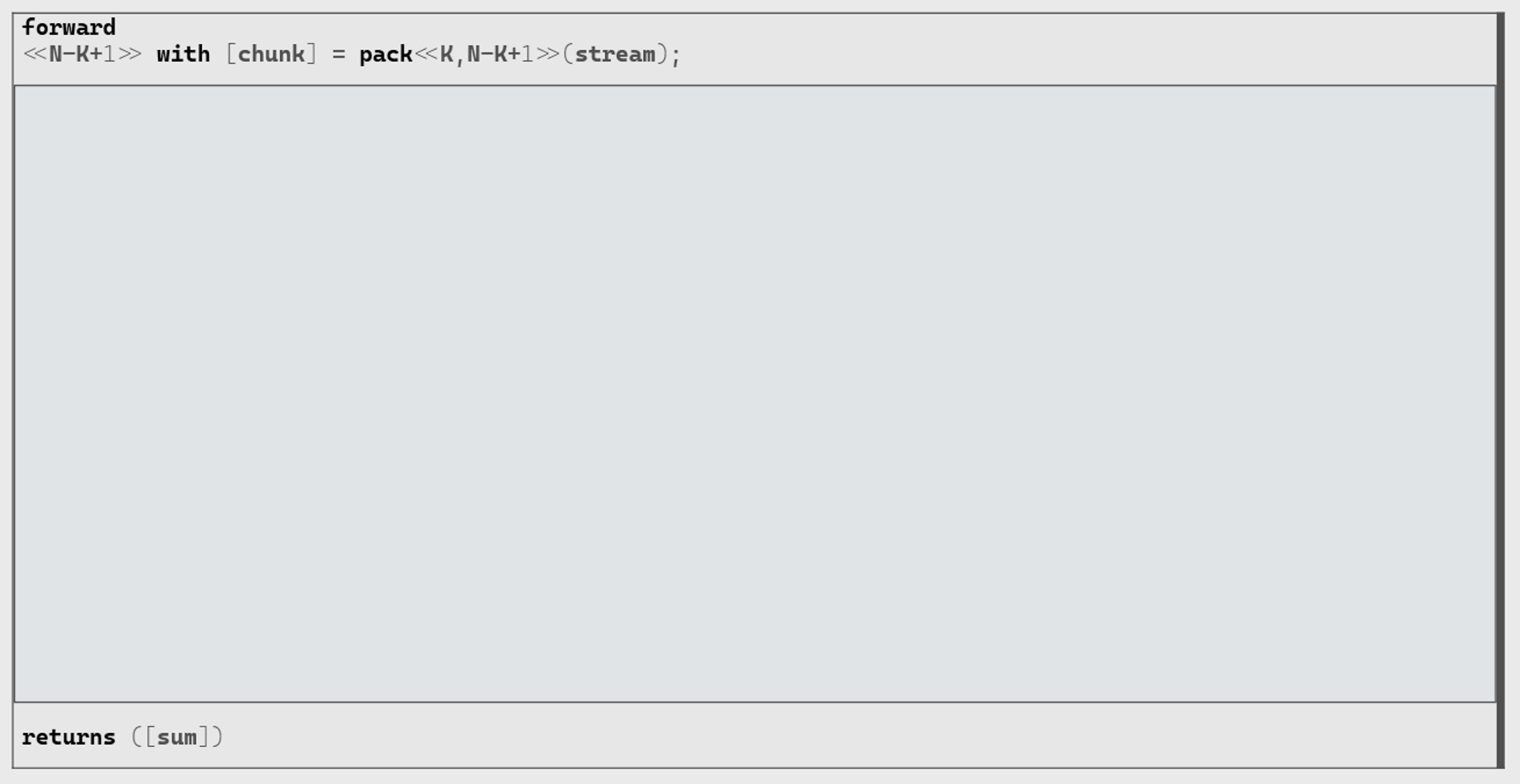
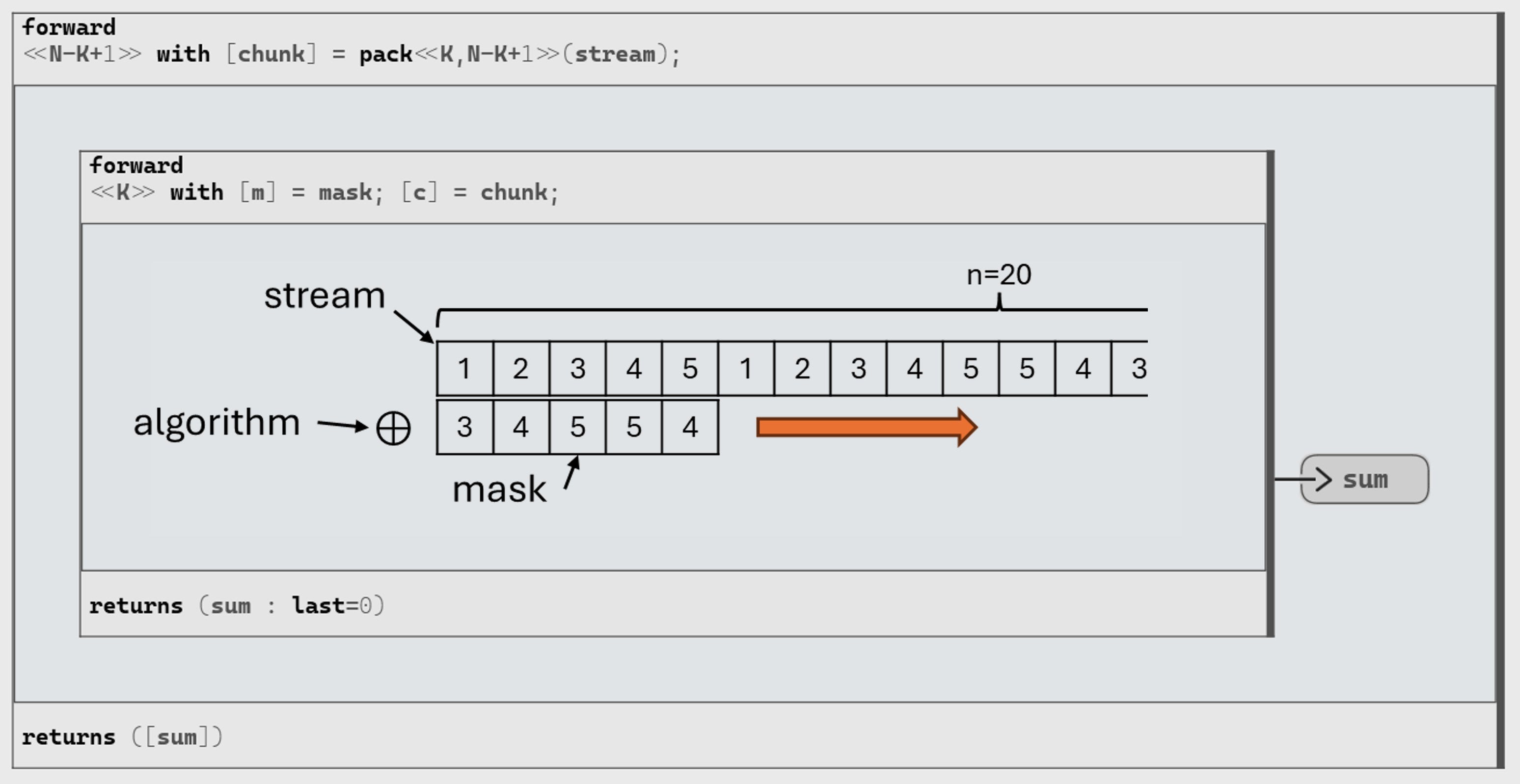
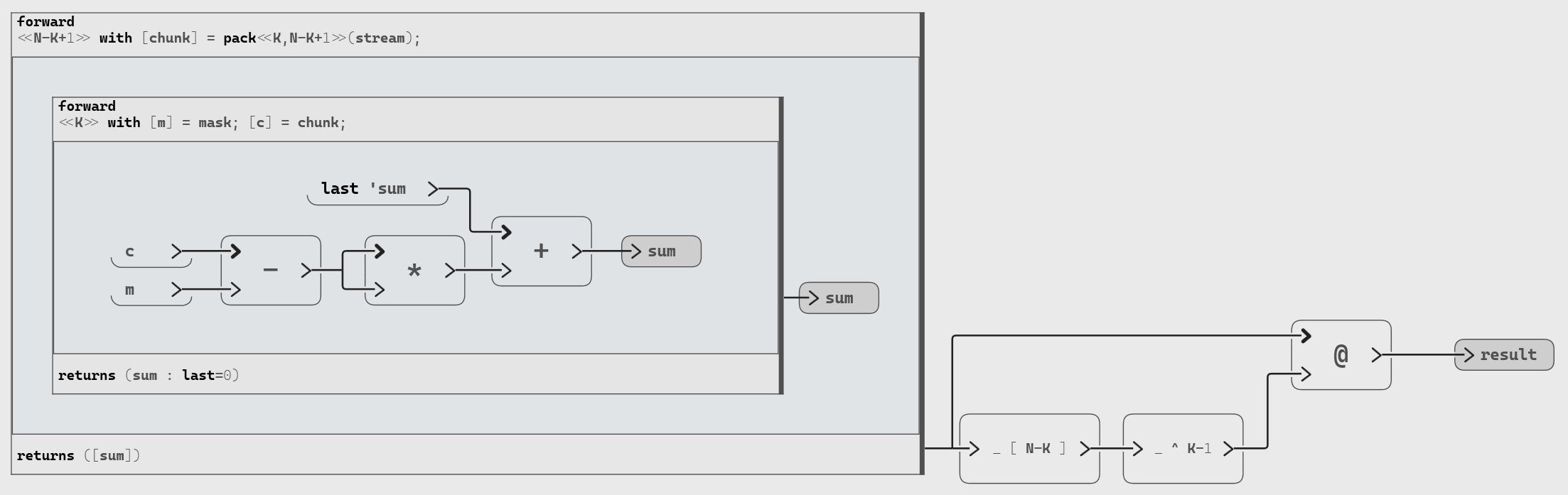
Step 1, we reshape stream A by using pack, as explained above, to propose a way to iterate safely with a forward loop.

With N = 20 and K = 5

Step 2, we apply our algorithm on each element of the chunk. Let’s cumulate the square of the difference between chunk and mask elements:

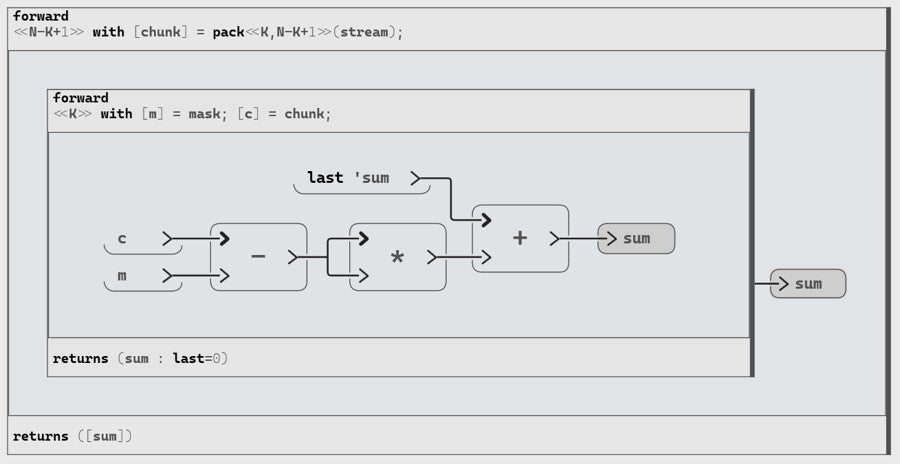
And finally, we fill in our algorithm to compute the difference of squares:

The resulting array of this operation is an array of size N-k+1.

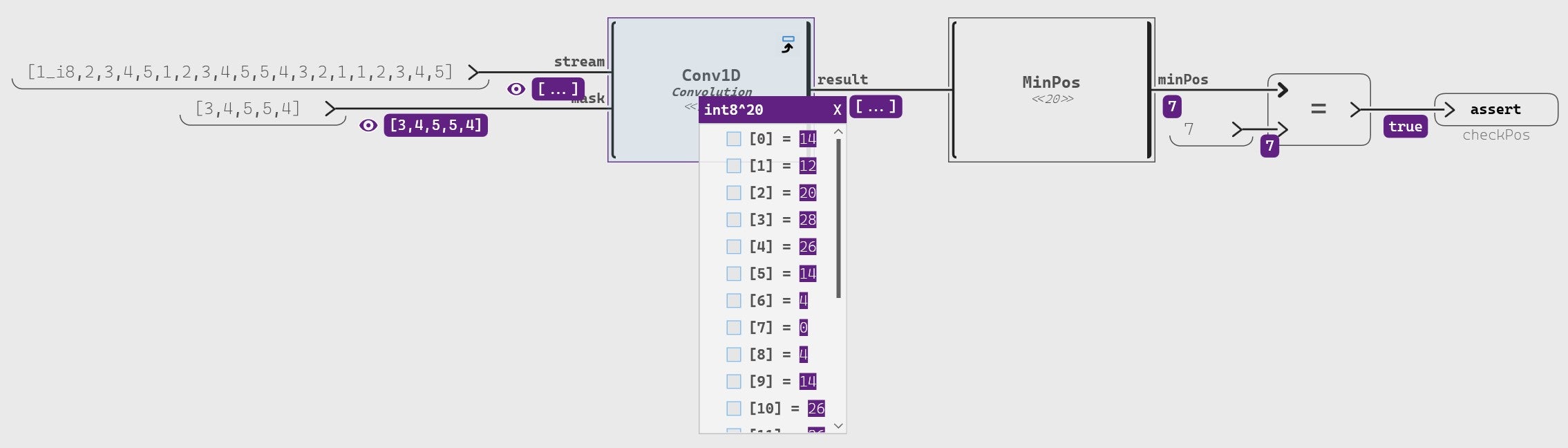
For consistency, let’s complete the output array by appending (@ operator) the end value to retrieve the same input size.

The resulting stream is the following. It measures, at each position, the gap between the mask and the input stream. The minimum value corresponds to the best match (least difference). A result of 0 corresponds to the perfect match (no difference).

Running a test in our Scade One model, we confirm that the above example finds a perfect match at index 7:

Using pack in two dimensions

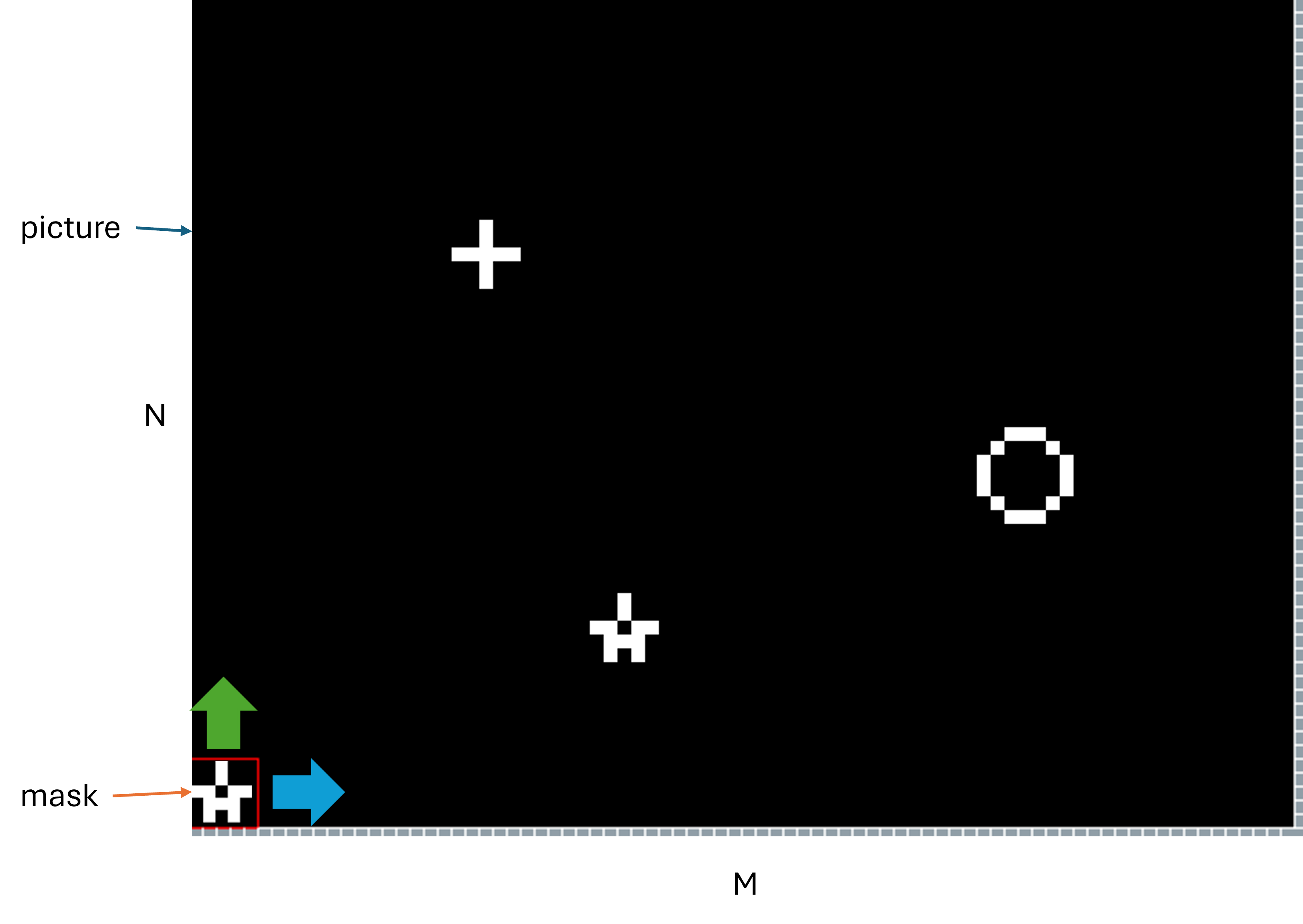
Let’s go back to our initial problem: detecting shapes in a 2D image. For this, we will use pack in two dimensions.

Here, the stream becomes a picture, implemented as a two-dimension matrix of type integer^COL^ROW.

The mask is a small square shape, implemented as a two-dimension matrix of type integer^K^K.

We must now determine the position of the mask shape in the picture:

Our aim is to visit all parts of the image with the same size as the mask and apply our algorithm on each one.

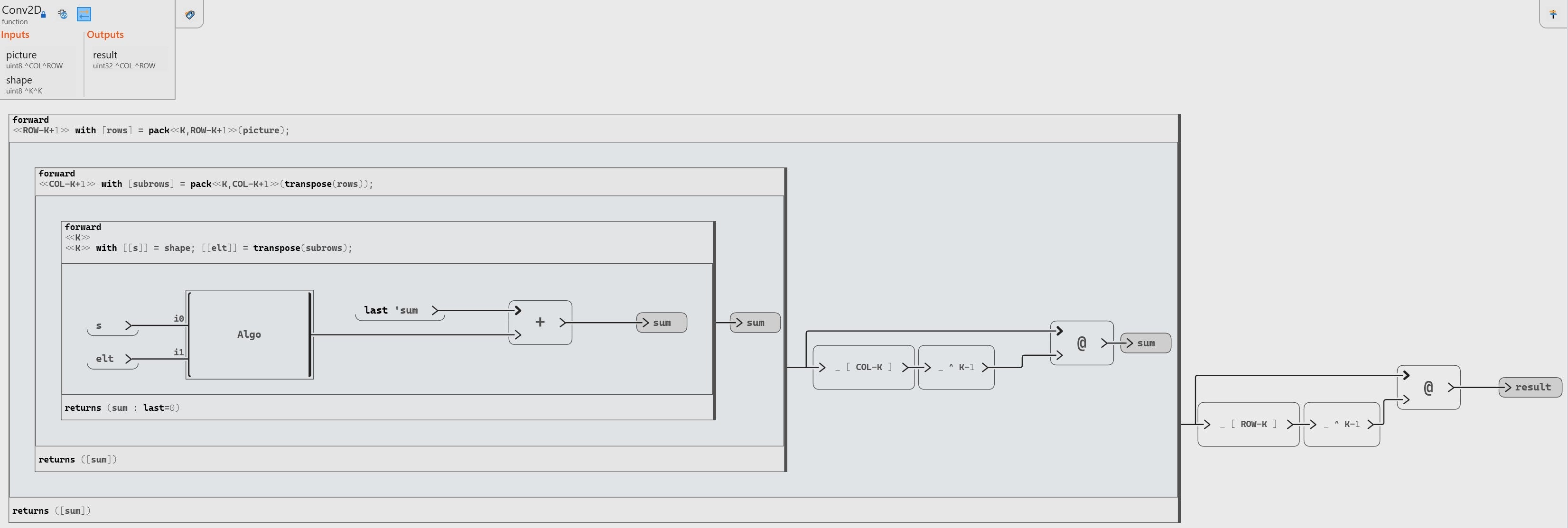
The picture has type integer^Col^Row and the mask has type integer^K^K.

We start by creating a pack of K rows, shifted by one row:

pack <‍<‍K, Row-K+1‍>‍>(picture) → integer^Col^K^(Row-K+1)

Then, we iterate on each pack:

forward <‍<‍Row-k+1‍>‍> with [lines] = pack<‍<‍K,Row-K+1‍>‍>(picture);

Now, we want to create a pack of K columns from lines → integer^Col^K:

To iterate on the second dimension Col, we must transpose the dimension: transpose(rows) → integer^K^Col

When applying pack on transpose(rows):

pack <‍<‍K, Col-K+1‍>‍>(transpose(rows)) → integer^K^K^(Col-k+1)

Our final form is:

forward <‍<‍Col-k+1‍>‍> with [subrows] = pack<‍<‍K,Col-K+1‍>‍>(transpose(rows));

We are now able to iterate on mask-sized subpictures, computing the difference between our mask and each subpicture.

Notice that here we use a square mask, and the dimensions seem good between the mask and the subpicture. All are matrices of type → integer ^K^K.

However, due to the previous transpose operation, mask dimensions are reversed; we must transpose our subpicture to realign it with the mask:

forward
<‍<‍K‍>‍>
<‍<‍K‍>‍> with [[s]]=shape; [[elt]]=transpose(subrows);

Here is our final operator:

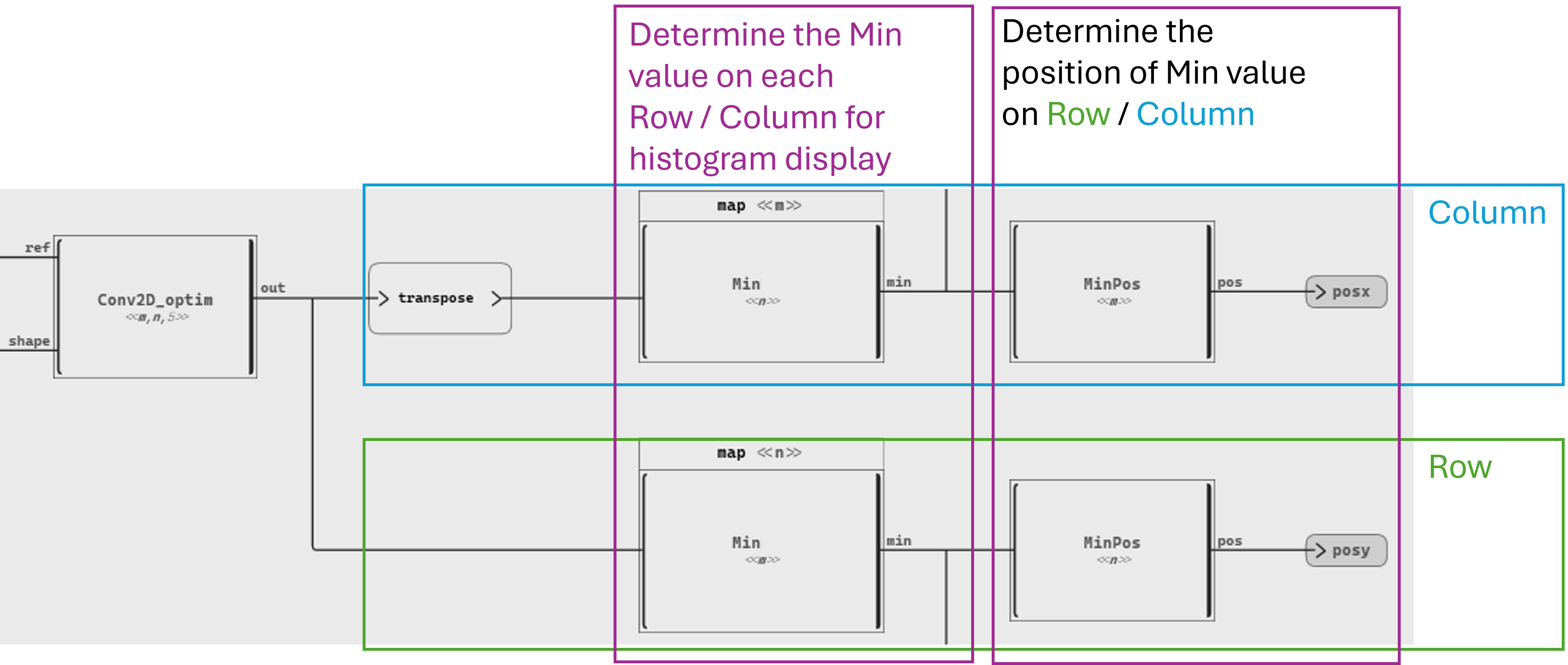
The resulting matrix measures, at each position, the difference between the mask and the input picture. The minimum value corresponds to the best match.

A naive approach to find this best match consists in extracting the position of the minimum value, cumulatively measured for each line and column.

Now that our implementation is complete, here is a video of our Scade One model in action, with a graphical panel showing what’s happening:

Conclusion

In this article, we demonstrated the use of the forward and pack Swan operators to solve a signal processing problem.

We saw that these operators enable clear, readable signal processing algorithms. By construction, the Swan language enforces safe array access, which allowed us to focus on our logic without worrying about skipping values or out-of-bounds errors.

Explore Further

Download the example in this blog here. If you are a SCADE user, you may access Scade One Essential with your existing licenses on the Ansys Download Portal and experiment with this example!

Learn more about the forward and pack blocks by visiting the Language Explanations section of the Scade One User Documentation.

Finally, you may schedule a live demo of Scade One using this link.

About the author

Mathieu Viala (LinkedIn) is a lead Application Engineer at Ansys. He has been supporting SCADE customers in early development phases, managing PoCs, training and post-sales support for more than 16 years.