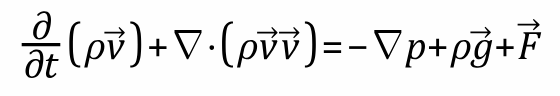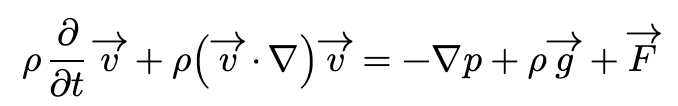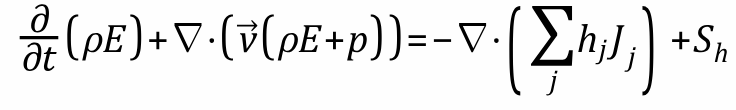Learning Forum

[stefankrischer]

Dear all,

I hope this is the right place for this question. I am currently writing my master’s thesis and a significant part of it are simulations in fluent. These are transient simulations of an axisymmetric setup with a single invicid compressible (ideal) gas. As I present these simulations in my thesis, I have to write a part on how fluent works and which equations are used. For this, the theory guide (2024 R2) is generally really helpful. But with two of the equations I have some problems.

At first the momentum conservation equations presented in chapter 1.7.1.2. which seems to have a kind of typo in Equation (1-35). There it is stated as

While in the Textbook that is referenced for a very simmilar equation in 1.2.2. states it as

 

Pulling the density into the deivates seems no problem for incompressible gasses and even for compressible gasses it is possible when arguing that the density does not vary much over one cell. But the position of one of the velocity vectors behind the nabla does not make sense in the theory guide, as far as I understand it. There are some weird things in the conversion of this equation into the axisymmetric case, but they might all be arguable with the only small variations over one cell.

But the even larger problem I've got with the energy conservation equation stated in chapter 1.7.1.3 as

Firstly, there seems to be the same issue with the misplaced velocity vector. But beyond that I don't understand why the pressure is added to the product of the density and the energy, this is not even possible as these don't have the same dimension.

I can not find this kind of equation or even anything similar in any textbook on the topic I searched. Does anyone know where this equation comes from and how it is formulated correctly? That would be really helpful!

Best Regards,
Stefan

[Essence]

 

Hello,

Could you please share the application you are working on? Thanks.

 

[Petros]

 

Hi, there is no typo in the equation of the Theory Guide. You get this form by applying Gauss’s theorem to convert the surface integral of the convective term:
\int_{CS}(\rho\vec{V} )\vec{V}\cdot\vec{n}dA 
to a volume integral:
\int_{CV}\vec\nabla\cdot(\rho\vec{V}\vec{V})dV

This is the general form and if incompressibility is assumed, applying Leibniz rule to the term in question, you drop the second term and you will get what you have in your Textbook.

As for the energy equation, this sum you are refering to is the internal energy. E has units of J/kg so the dimensions are fine. Section 1.2.1.3 of CFX Theory Guide, explains how to obtain this form.