Learning Forum

[c455km]

My question is regarding the calculation of the strain tensor in LS-prepost. Let's consider the problem of pure shear in a linearly elastic formulation (*MAT_ELASTIC). According to the material model, the shear components of stress and strain tensors should oscillate. Indeed, the shear components of the stress tensors (element time history) and elastic deformations (fringe component) oscillate, but the shear component of the strain tensor (element time history) is monotonous. Agree that such a difference in the interpretation of the strain tensor in a linear formulation is rather ridiculous. Moreover, the problem disappears immediately if we build a strain tensor by confrontational integration of the strain rate tensor (in the sense of Jaumann). The correctness of this approach is confirmed in LS-DYNA Theory Manual R14 (21.10 String Output to the LS-DYNA Database, formulas 21.54 - 21.57). Why this is not

 

 

 

implemented in ls-prepost is completely unclear.

[Alex Rycman]

Hello, 

Could you please check the STRFLG flag in *DATABASE_EXTENT_BINARY. It looks like the xy strain graph is engineering strain, setting STRFLG = 1 will write a cauchy strain tensor to elout. 

Please let me know if that helps. 

Thank you,

Alex 

[c455km]

Of course, STRING = 1 is set. And this does not eliminate the question of an incorrect representation of the strain tensor in the linear elastic case.

[Alex Rycman]

Hello, 

Which strain is being plotted? 

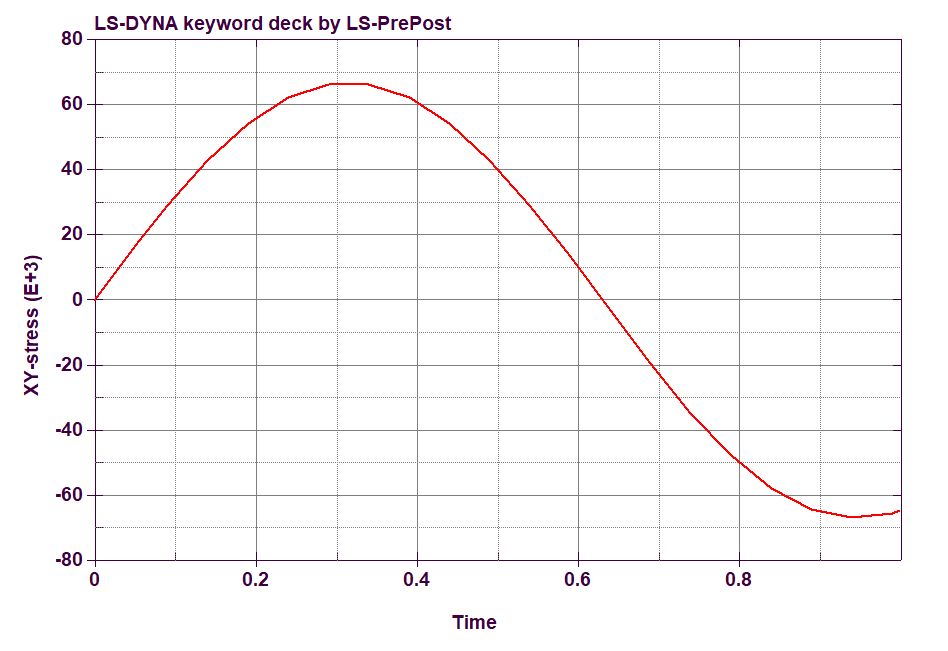
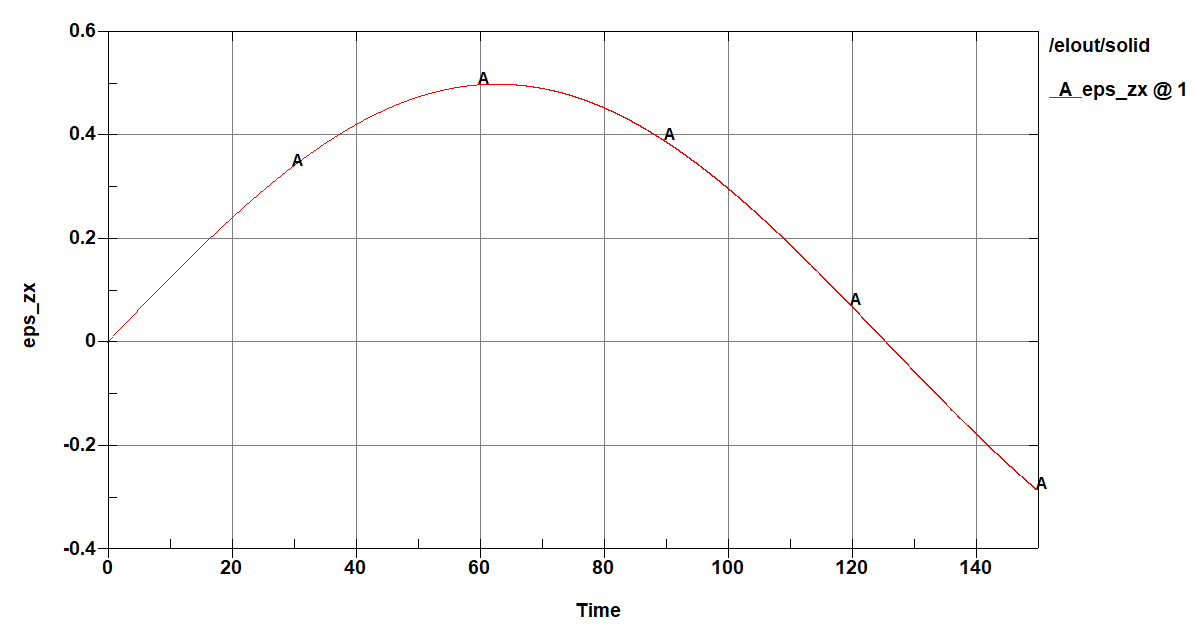
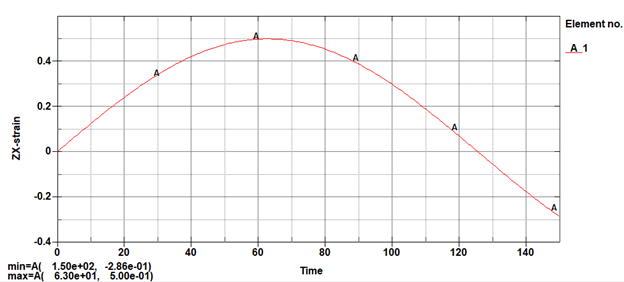
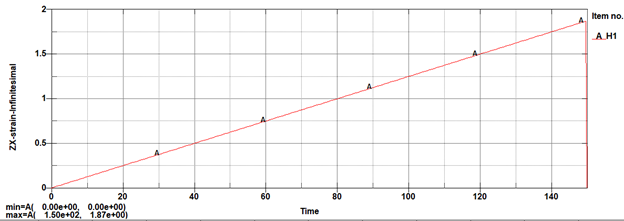
After running a simple shear model and plotting the strains I got the following results. If the Cauchy strain is plotted (computed by LS-DYNA), the graph should look like this:

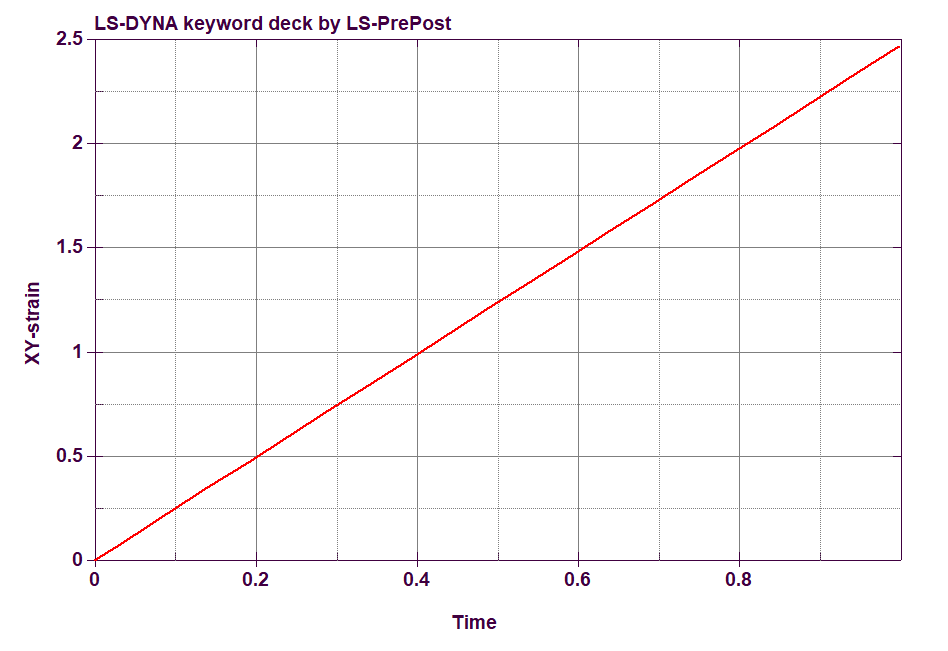
If the engineering (infinitesimal) strain is plotted (computed by LS-PrePost) it will be of course linear: 

 

Please check exactly which strain is being plotted. 

 

Thank you,

Alex 

[c455km]

The question was that the elastic strain tensor and the total strain tensor do not exist in this problem. The elastic strain tensor is not equal to the Cauchy-Green tensor. As for the infinitesimal strain tensor, it is not applicable to the case of finite deformations.