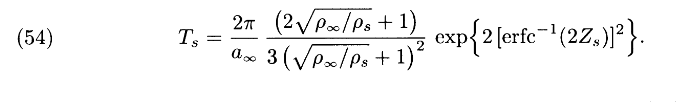-
-
February 19, 2024 at 10:33 pm
hmanatunga
SubscriberDear Fluent Combustion community,
In the Fluent's Theory Manual Section 8.1.4.2.3 Embedding Diffusion Flamelets in Turbulent Flames, I have noticed that the Favre mean scalar dissipation rate ($\chi_{st}$) is modelled as $\tilde{\chi_{st}}=2 \frac{\widetilde{f^{'2}} \tau}$ where $\tau$ is the time scale and and the Favre mean of the mean mixture fraction variance is \widetilde{f^{'2}}.. According to literature, (example Theoretical and Numercial Combustion by Poinsot and Veynante) this is not correct and is equal to the mean of the scalar dissipation rate ($\tilde{\chi}$).

$\tilde{\chi_{st}}$ field need then be obtained from $tilde{\chi} field using the following relationship
Has anyone else noticed this? Should this be corrected?
Also according to the manual, the modelling method that is used to model the $\chi$ across the flamelet is attributed to the paper by Kim and Williams - "Extinction of diffusion flames with nonunity Lewis numbers", 1997. (DOI: https://doi.org/10.1023/A:1004282110474). After reading this paper, I couldnt find anything about scalar dissipation rates or diffusion timescales. But their previous paper "Structures of Flow and Mixture Fraction Fields for Counterflow Diffusion Flames with Small Stoichiometric Mixture Fractions", 1993, presents a formula for $T_{s}$ (eq 54 below) which is the diffusion time at the location of the flamelet where the mixture fraction is equal to the mixture fraction at stoichiometry. Inverse of this would give the scalar dissipation rate at stoichiometry.I am confused as to how the Fluent theory manual arrived at Eq. 8-43 (section 8.1.4.3 Flamelet Generation).
I appreciate any light that the combustion community can shed on this matter! ????
Thanks! Mana -
February 20, 2024 at 11:10 pm
hmanatunga
SubscriberOk I have a bit more clarity on this after re-reading the Fluent manual article a few more times. I think, Kim and Williams' formulation of $\chi$ (indicated in the original posting as Eq. 8-43 of the fluent theory manual and the closest formulation that I can find in literature:Eq.54, is used purely to calculate the $\chi$ across the flamelet. This is clearly written in the manual . (I must have overseen it in the first few sweeps).
Since the Theory Manual assumes that the $\tilde{\chi_{st}}$ is modelled as indicated Eq. 8 -45 in the original post there is no need to explicitly calculate the $\tilde{chi_{st}}$ using the below approach. Do I understand this correctly?
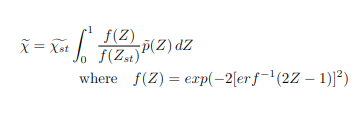
-
February 23, 2024 at 6:10 am
vinaraya
Ansys EmployeeHi Manahara, The Eq.8-43 corresponds to the chi-stoic and Eq. 8-49 corresponds to the distribution of chi across the flamelets as you rightly mentioned. Eq. 8-50 indicates how the instantaneous chi can be related to chi-stoic (using Eq. 8-43). But when we go to the Turbulent flames, chi is assumed to have a delta distributon and it is related to mean chi-stoic. Eq 8-45 indicates how fluent models the mean chi-stoic.
To summarize, Flunet assumes the Eq 8-45 to model mean chi-stoic.
-
February 26, 2024 at 4:04 am
hmanatunga
SubscriberHi Vijay, Thank you for taking the time to respond to my query.
I am basing my understanding of the Steady Diffusion Flamelet concept entirely on the book by Thierry Poinsot and Denis Veynante, called "Theoretical and Numerical Combustion". The following is a summary I made of how this book explains the Steady Diffusion Flamelet concept assuming there are no fluctuations of chi_st along the flame front. (which itself is a problematic assumption, or so I am beginning to find out).
The assumption here is that the pdf of chi_st is assumed to be a delta function and NOT chi.
I believe that assuming that pdf shape of chi itself to be a delta function and also to simply assume that chi mean is equal to chi_st mean is fundementally wrong.
Can you please verify that your comment "Eq 8-45 indicates how fluent models the mean chi-stoic." is infact how the chi_st is calculated in Fluent. Can thus exactly be verified with respect to how the Fluent code is written?
Does this mean that the Fluent scalar field 'scalar-dis' is mean chi_st and not mean chi?
Thanks again for looking into this for me.
Mana -
March 1, 2024 at 6:32 am
vinaraya
Ansys EmployeeHi Mana,
From the snippet you shared, the mean_chi is pointing to the same formulation which fluent is assigning to mean_chi_stoic. As there seems to be a discrepancy between the two, I will check with the team and revert back.
Regards,
Vijay
-
March 28, 2024 at 7:23 am
hmanatunga
SubscriberHi Vijay, Do you have any further updates on this? Thanks! Mana
-
April 10, 2024 at 6:02 am
vinaraya
Ansys EmployeeHi Mana,
A Support ticket has been raised for this query and I'm looking in it. I will update you soon.
-
- The topic ‘Flamelet Model $\chi_{st}$ calculation’ is closed to new replies.



-
4818
-
1587
-
1386
-
1242
-
1021

© 2026 Copyright ANSYS, Inc. All rights reserved.