Physics Setup — Lesson 5
In the Workbench window, this is what you should see currently in the Project Schematic space:
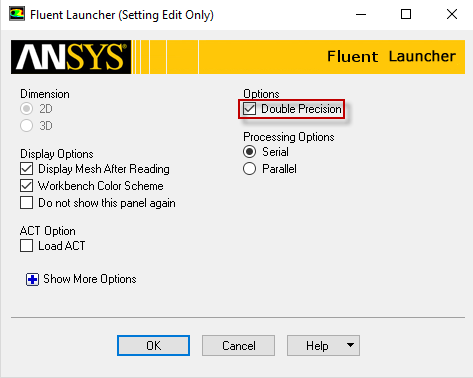
Double click on Setup, which will bring up the Fluent Launcher. When the Fluent Launcher appears change the options to "Double Precision" and then click OK as shown below. The Double Precision option is used to select the double-precision solver. In the double-precision solver, each floating point number is represented using 64 bits, in contrast to the single-precision solver which uses 32 bits. The extra bits increase not only the precision but also the range of magnitudes that can be represented. The downside of using double precision is that it requires more memory.
Twiddle your thumbs a bit while the Fluent interface comes up. This is where we'll specify the governing equations and boundary conditions for our boundary value problem. On the left-hand side of the Fluent interface, we see various items listed under Setup. We will work from top to bottom of the Setup items to set up our boundary value problem. On the right-hand side, we have the Graphics pane and, below that, the Command pane.
Display Mesh
Let's first display the mesh that was created in the previous step.
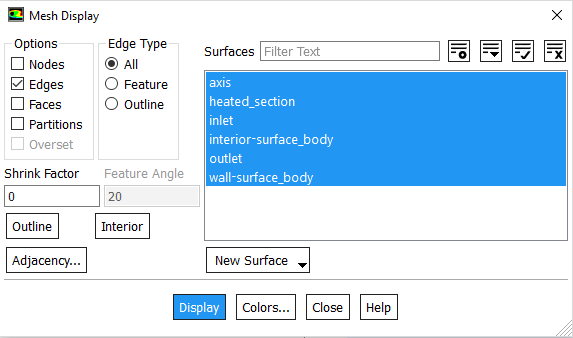
Setup > General > Mesh > Display...
The long, skinny rectangle displayed in the graphics window corresponds to our solution domain. Some of the operations available in the graphics window to interrogate the geometry and mesh are:
Translation: The model can be translated in any direction by holding down the Left Mouse Button and then moving the mouse in the desired direction.
Zoom In: Hold down the Middle Mouse Button and drag a box from the Upper Left-Hand Corner to the Lower Right-Hand Corner over the area you want to zoom in on.
Zoom Out: Hold down the Middle Mouse Button and drag a box anywhere from the Lower Right -Hand Corner to the Upper Left-Hand Corner.
Use these operations to zoom in and interrogate the mesh.
You should have all the surfaces shown in the above snapshot. Clicking on a surface name in the Mesh Display menu will toggle between select and unselect. Clicking Display will show all the currently selected surface entities in the graphics pane. Unselect all surfaces and then select each one in turn to see which part of the domain or boundary that surface entity corresponds to (you will need to zoom in/out and translate the model as you do this). For instance, the surface labeled heated_section should correspond to the part of the wall where heating occurs.
Specify Governing Equations
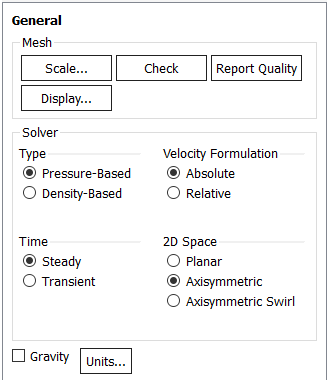
We ask Fluent to solve the axisymmetric form of the governing equations. When you do this, the solver switches to cylindrical polar coordinates. So, from here on, you should interpret the horizontal coordinate as axial and the vertical coordinate as radial.
General > Solver > 2D Space > Axisymmetric
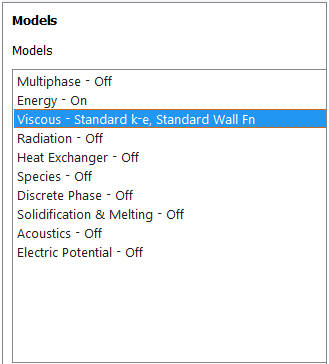
The energy equation is turned off by default. Turn on the energy equation. Note that in most cases, you'll have to double-click on an item to select it.
Models > Energy - Off > Edit...
Turn on the Energy Equation and click OK.
By default, Fluent will assume the flow is laminar. Let's tell it that our flow is turbulent rather than laminar and that we want to use the k-epsilon turbulence model to simulate our turbulent flow. This means Fluent will solve for mean (i.e., Reynolds-averaged) values of velocity, pressure, and temperature. It will add the k and epsilon equations to the set of governing equations to calculate the effect of the turbulent fluctuations on the mean, as discussed in the Pre-Analysis step.
Models > Viscous - Laminar > Edit...
Under Model, select k-epsilon (2 eqn). Since we'll use the default settings for the k-epsilon turbulence model, click OK.
This is what you should currently see under Models.
Now let's set the "material properties," i.e., properties of air that appear in our boundary value problem.
Materials > Fluid air > Create/Edit...
Since variations in absolute pressure are small in our pipe, we'll use a constant absolute pressure in the ideal gas law as discussed in the Pre-Analysis step. This is called the "incompressible ideal gas" model in Fluent (it's non-standard nomenclature). Change the Density (kg/m3) from constant to incompressible-ideal-gas. The constant absolute pressure to be used in the ideal gas equation is specified later as Operating Pressure.
The other properties are also functions of temperature. However, we'll use constant values equal to the average values over the temperature range obtained in the experiment. Enter the following constant values:
Cp (Specific Heat) (j/kg-k): 1005
Thermal Conductivity (w/m-k): 0.0266
Viscosity (kg/m-s): 1.787e-5
Molecular Weight (kg/kgmol): 28.97
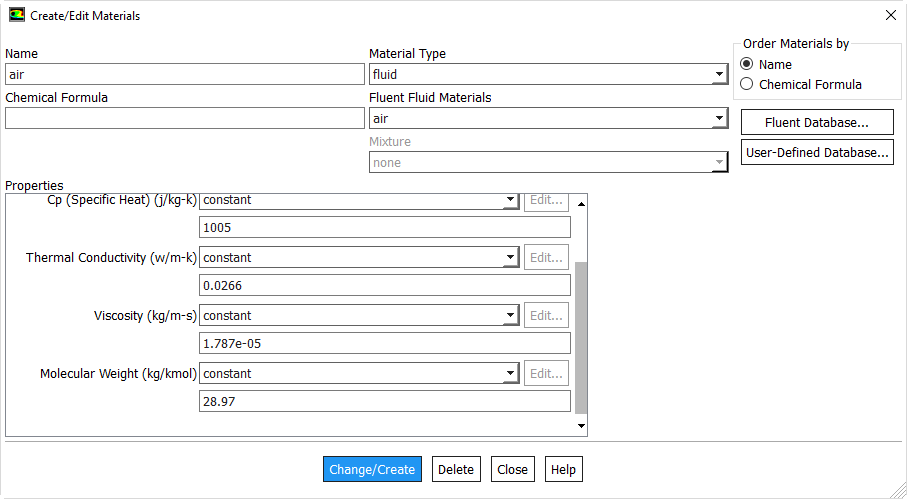
Click Change/Create and Close the Create/Edit Materials window.
Specify Boundary Conditions
Fluent uses gauge pressure internally to minimize round-off errors stemming from small differences of big numbers. Anytime an absolute pressure is needed, it is generated by adding the so-called "operating pressure" to the gauge pressure:
absolute pressure = gauge pressure + "operating pressure"
This "operating pressure" is also used in the "incompressible ideal gas" model as mentioned above. We will specify the "operating pressure" as equal to the measured ambient pressure since the absolute pressure in the pipe varies only slightly from this (you do get significant variations in gauge pressures though).
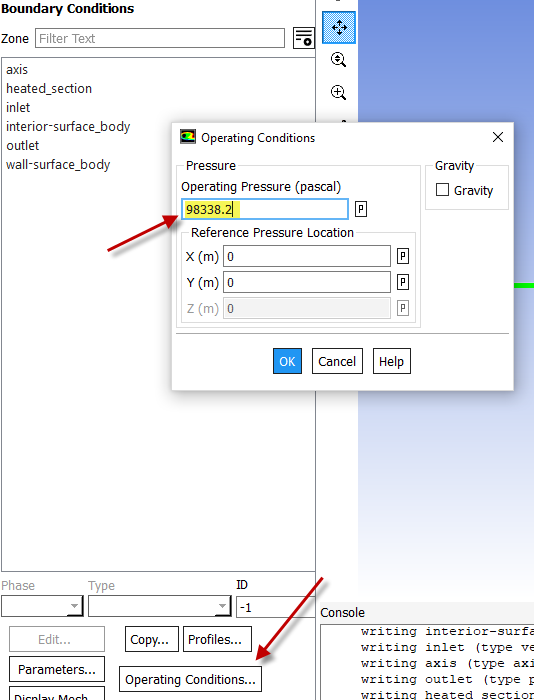
(double-click) Boundary Conditions > Operating Conditions...
Enter 98338.2 under Operating Pressure and click OK.
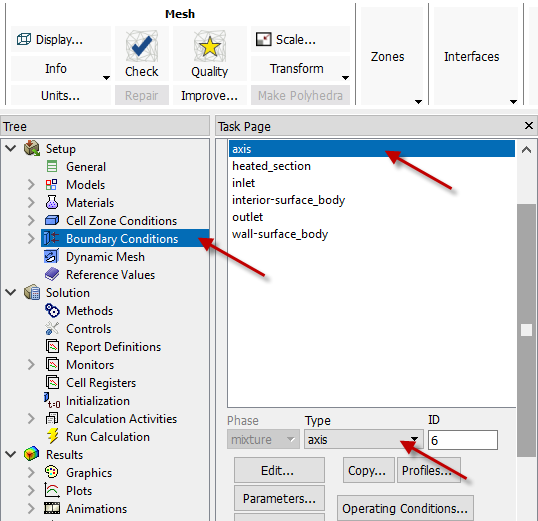
Next, we will specify the boundary condition for the centerline.
Boundary Conditions > axis
Change the Type to axis and click OK. Fluent will set all radial derivatives at this boundary to zero in accordance with the axisymmetric assumption.
Now, let's specify the boundary condition at the walls. By default, Fluent correctly picks the Wall boundary type for these boundaries. It will impose the no-slip condition for velocity at these boundaries. Additionally, for the heated wall section, we need to specify the heat flux into the flow.
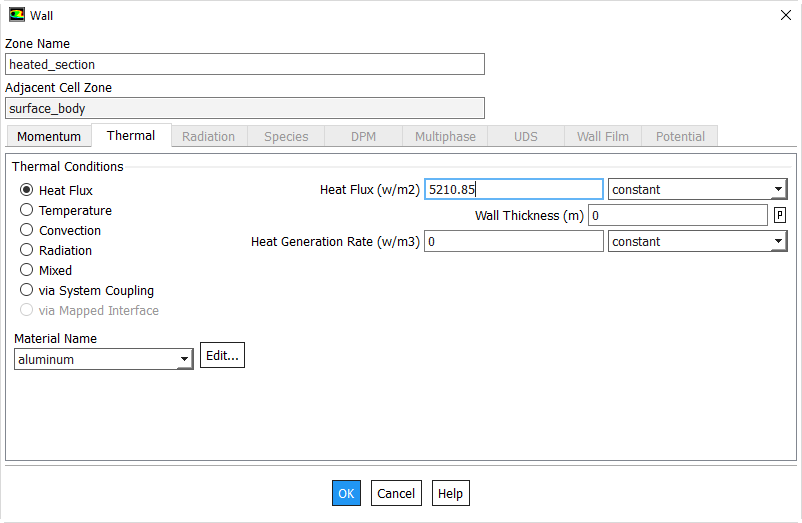
Boundary Conditions > heated_section > Edit...
A new Wall window will open. Click on the Thermal tab and enter 5210.85 next to Heat Flux (w/m2) and click OK.
As discussed in the Pre-Analysis step, we need to set:
- Velocity and temperature (plus k and epsilon for the turbulence model equations) at the inlet
- Pressure at the outlet
For subsonic flow, the flow adjusts to the pressure at the outlet (consider this as a signal you are sending the flow about what it needs to do inside the pipe).
Select:
Boundary Conditions > inlet
Note that the boundary Type is automatically set to velocity-inlet. Fluent has an automatic mechanism to pick a boundary type according to the name you give and settings that you have selected previously (this can be dangerous if Fluent selects the wrong boundary type and a lackadaisical user doesn't change it). In this case, it gets it right.
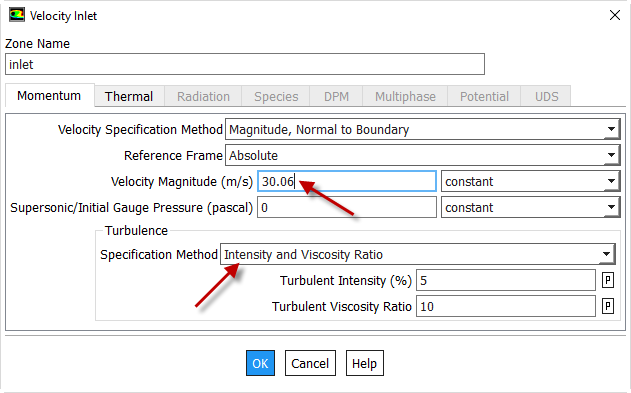
Click Edit... to set up the correct inlet parameters. The Velocity Inlet window pops up. Enter 30.06 next to Velocity Magnitude (m/s). Under Turbulence, select the specification method to be Intensity and Viscosity Ratio.
Use the default values for Turbulent Intensity (5%) and Turbulent Viscosity Ratio (10). These are plausible guesses for the turbulence level at the inlet. Fluent will calculate k and epsilon at the inlet from these values and use them as boundary conditions for the k and epsilon equations. The results should not be sensitive to these inputs since most of the turbulence is generated in the boundary layers (ideally, you should check the sensitivity of your calculation to this setting).
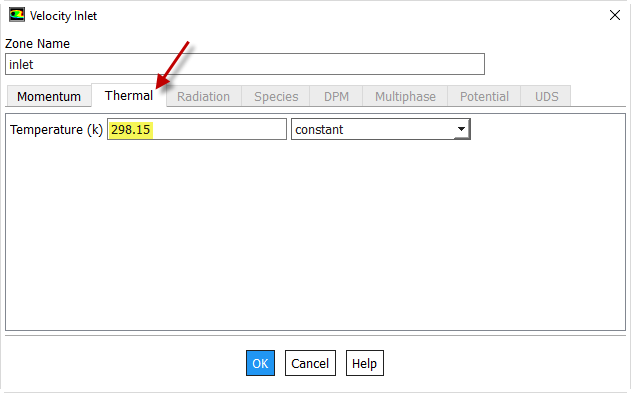
Now click on the Thermal tab and enter 298.15K for Temperature. Click OK to close the window.
Finally, set up the outlet boundary condition:
Boundary Conditions > Outlet
Fluent selects the pressure-outlet boundary type and its guess turns out to be right.
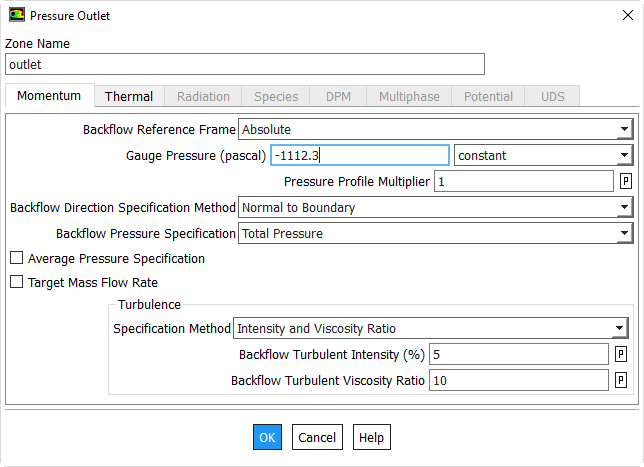
Click Edit... to specify the gauge pressure at the outlet.
Enter -1112.3 for Gauge Pressure and click OK. (From experiment, measured outlet pressure is 97225.9 Pa corresponding gauge pressure = 97225.9 Pa - operating pressure = -1112.3 Pa.) The negative sign indicates that the pressure at the outlet is lower than the ambient value.
Now Fluent knows all necessary elements of our beloved BVP (domain, governing equations, and boundary conditions). In the Solution step, we'll prod the beast to obtain an approximate numerical solution to our BVP.

