Numerical Results — Lesson 7
Instructions for Cornell students: Cornell MAE 4272 Fall 2020: For the canvas quiz, you should use the Fluent inputs from this tutorial. Later, you will need to repeat the Fluent simulation with inputs from YOUR MEASUREMENTS in the lab and compare the Fluent results with the experiment.
Temperature Contour
The following video shows how to create a temperature contour in CFD-Post.
Summary of the Above Video:
- Create a Contour Plot and name it Temperature Contours
- Under Geometry > Locations, choose periodic 1 and set the variable of interest as Temperature
- Under View > Apply Scale, enter (1, 30, 1)
- Default Transform
- Apply Reflection about ZX Plane
You can save the image to a file using the camera icon indicated in the image below or using the Snipping Tool in Windows (you can search for it under Start > Programs).
In developing the experiment, it was assumed that by the end of the adiabatic mixing stage, the flow will be well-mixed. Do the results from the numerical solution simulation support this assumption?
Velocity Vectors
The following video shows how to create velocity vectors along the pipe in CFD-Post.
Summary of the Above Video:
- Click Vectors > Name Velocity Vectors
- In Details, plot Velocity
- In Variable > Color by Variable
- Color by temperature
We see that the flow speeds up as the density decreases in order to keep the same mass flow rate.
Does the flow become fully developed at the end of the first section?
Wall Temperature Plot
In the following video, we will create graph of wall temperature.
Summary of the Above Video:
- Create location > Line
- Point 1: (0,.0294,0) Point 2: (6.045,.0294,0)
- Create Chart
- Under Data Series > Location Select line you just created
- X Tab
- Plot X location
- Y Tab
- Plot Temperature
The wall temperature values can be exported to a csv file (suitable for Excel) using the Export button highlighted below.
Importing Experimental Data and Chart Formatting
We can import experimental data from a csv file using the procedure shown below. The csv file should contain two columns, corresponding to the x-axis and y-axis values, respectively
Summary of the Above Video:
- In details of Chart > New Series > Import Data from file
- Find file and click okay
- Change how experimental data looks in CFD Post
- In Line Display under Series 2 > No Line > Symbols > Ellipse
- Chart Details > General
- Give Title
- Chart Details > Chart Display
- Font Sizes
- Grid Sizes
Note that the centerline temperature and pressure variations can be plotted by duplicating this plot as mentioned in the video.
Mixed Mean Temperature at an Axial Location
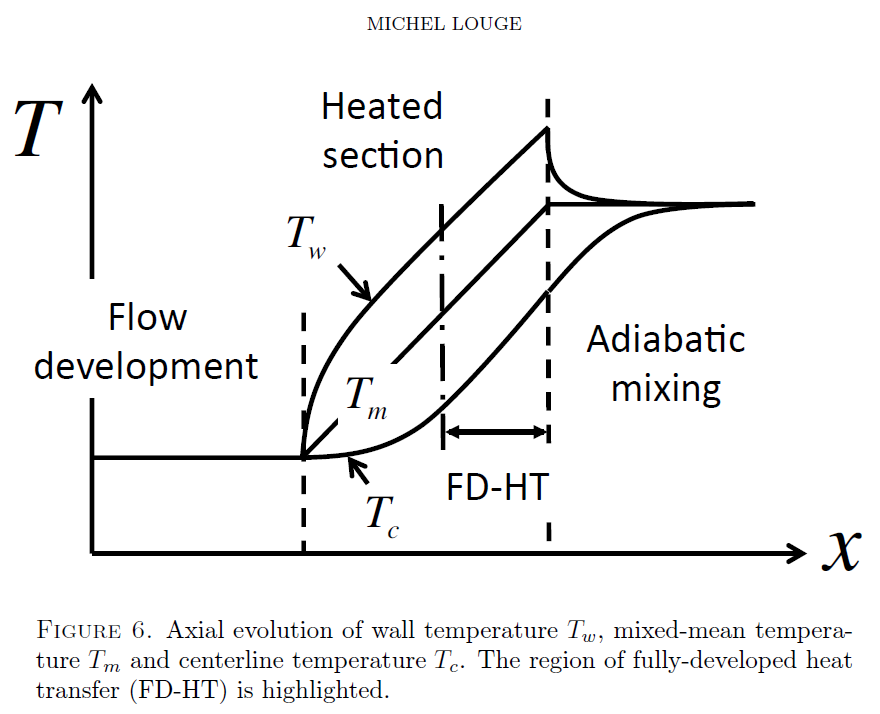
From energy conservation, we can show that the mixed mean temperature is constant in the flow development and mixing sections and varies linearly in the heated section. This is shown schematically in the following figure from the MAE 4272 lab manual.
The slope of Tm in the heated section can be obtained from the following equation, which is derived from the energy balance in the heated section:
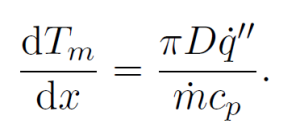
Using the above equation, calculate the mixed mean temperature Tm at x=2.67 m. Remember to add the inlet temperature, otherwise you will just end up with the temperature difference between the mixed mean temperature and the inlet temperature (where we assumed the flow was fully mixed). An alternative procedure to calculate Tm involves integrating the temperature profile. This procedure is covered in the Verification & Validation section in the video entitled Check Energy Conservation via Mixed Mean Temperature Variation. If energy is conserved in the Fluent simulation, the values calculated using the two procedures should match.
Wall Temperature at an Axial Location
For calculating the Nusselt number at an axial location, we need the wall temperature at that location. The wall temperature at an axial location can be calculated in two ways:
- By interpolating the Tw vs. x values exported to Excel from the wall temperature plot obtained above
- By directly extracting the wall temperature at the desired location using the Probe function in the post-processor
The following video shows you the procedure for extracting the wall temperature at x=2.67 m using the Probe function; this value can then be used to calculate the Nusselt number. To repeat the calculation at a different axial location, you can right-click on appropriate items in the tree, duplicate and modify as necessary. You need to double-click on an item in the tree to modify it; this is easy to overlook.
Summary of the above video:
- Create a line at x = 2.67
- Go to Expressions, right click and click New
- Name Tw267
- Right click in Definition box > Functions > CFD-Post > maxVal
- Right click within the parenthese of maxVal > Variables > Temperature
- Right click after the @ sign > Locations > x267
Nusselt Number
Instructions for Cornell students: Cornell MAE 4272 students, Fall 2020: Please use the following procedure for calculating the Nusselt number at two axial locations in the heated section where the flow is thermally fully developed.
The convective heat transfer coefficient, h, can be determined from Newton's law of cooling:

The wall heat flux on the left-hand side is known from the boundary condition. We have shown you how to get the wall temperature Tw at an axial location. Calculate the mixed mean temperature at the same axial location by evaluating the following integral using the procedure shown in the video in the Verification & Validation section. The title of the video is Check Energy Conservation via Mixed Mean Temperature Variation.
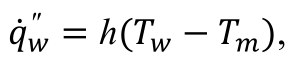
Once you determine h, you can non-dimensionalize it to get the Nusselt number.
The Nusselt number in the thermally fully developed region should be the same at different axial locations. Why? Do your Nu values at the two axial locations compare reasonably well? Why or why not?
Wall Shear
We plot the wall shear using the procedure shown in the video below.
Summary of the above video:
- Click on the Chart Viewer tab
- Click chart in the top toolbar
- Name it Wall Shear
- Click on Data Series Tab
- In Location dropdown menu, choose Wall
- Click on X Axis tab
- under Variable, choose X
- Click on Y Axis tab
- under Variable, choose Wall Shear X or Wall Shear
- Go to Location in the tree
- Double click on Wall
- Increase Sampling from 50 to 200
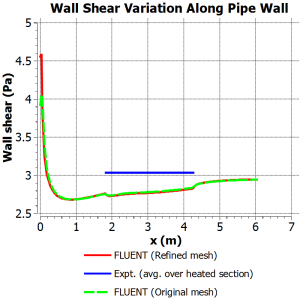
We then consider the trends in the wall shear in the heated, mixing, and flow development sections and try to justify them through physical reasoning.
You can spiff up your plot using the tips discussed below. This video also shows you how you could read in experimental results for comparing the wall shear between simulation and experiment.
Summary of the above video:
- To edit how the Wall shear graph is displayed
- Select Wall shear in tree
- Click on General, check Title and enter title in Title blank
- In Data Series, enter series name in Name blank
- In X Axis, enter x axis label in Custom Label blank
- Same for Y Axis
- In Line Display, uncheck "Use series..." and type within Legend Name blank
- In Chart Display, under Sizes, toggle with the line sizes and font
- To add another data series
- Go to Data series tab of Wall Shear
- Click on New button
- Scroll down, click File as Data Source > browse for your file
- To export the chart
- Click the button next to undo
- Select location to save
- Rename
When the simulation was repeated for conditions for which experimental data are available, we got the comparison shown below. The difference in the average wall shear in the heated section between the simulation and experiment is a respectable 4%. Note that the wall shear in turbulent flows is difficult to predict accurately due to the steep velocity gradients at the wall.
Fanning Friction Factor
The Fanning friction factor, also called the skin friction coefficient, is obtained by non-dimensionalizing the wall shear. It can be calculated and plotted using the procedure outlined below.
Summary of the above video:
- Create Location > Point
- (2.67, .0294, 0)
- Probe wall shear at point:
- Create Expression > Right Click > New Expression
- Probe(Wall Shear)@w267 / 1.483 (Pa/K) /Tm267
- Can duplicate for different locations for a plot
Final Plots
Input Summary
In older versions of Fluent, you can view the input summary (model, material properties, boundary conditions, etc.) by clicking on Report in the menu bar of Fluent. A small window will pop up and you can print the selected input summary directly in Fluent.