Contoh Simulasi — Aliran Tak Termampatkan Melalui Nosel Konvergen
Ringkasan
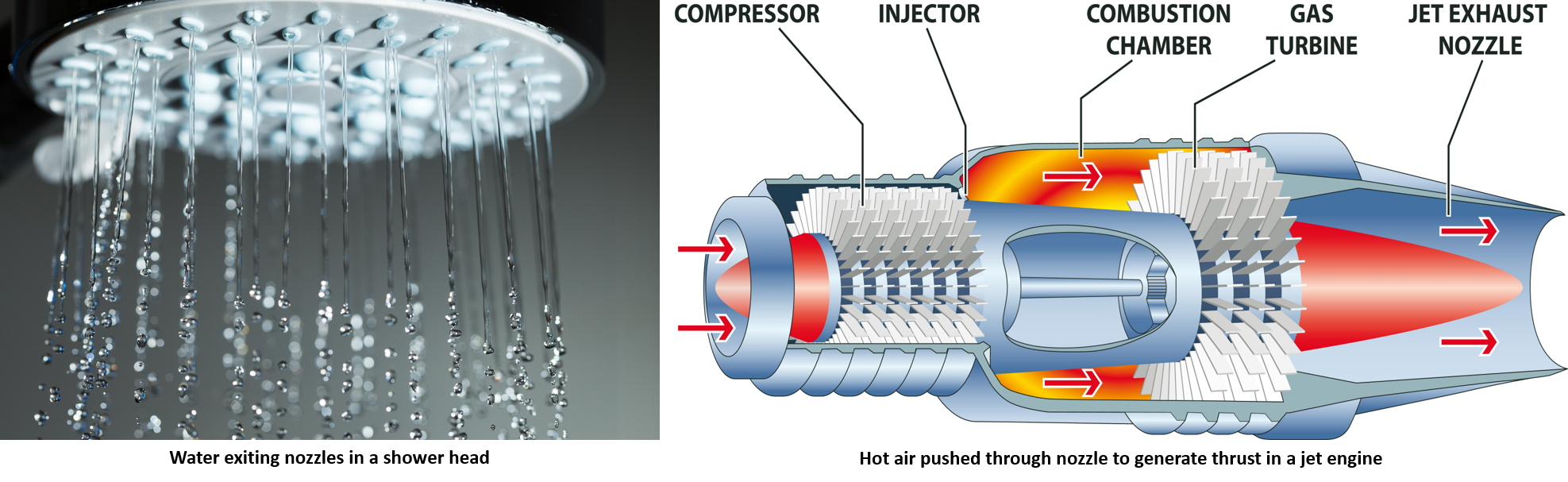
Dari alat penyiram air dan sistem vakum hingga kompor gas dan jacuzzi hingga karburator dan sistem semprotan bahan bakar, nosel umum digunakan di banyak aplikasi teknik. Nosel adalah konfigurasi geometris dari berbagai luas penampang yang dimaksudkan untuk mengontrol sifat karakteristik fluida yang mengalir melaluinya. Mereka paling sering digunakan untuk memodifikasi (meningkatkan) velositas aliran fluida. Pada intinya, nosel bekerja berdasarkan prinsip kekekalan massa dan momentum. Untuk aliran inkompresibel di mana densitas konstan, kekekalan massa menentukan bahwa velositas fluida berbanding terbalik dengan luas penampang nosel. Ini berarti bahwa ketika luas penampang nosel berkurang, velositas fluida meningkat. Jika kita selanjutnya mengasumsikan bahwa viskositas fluida dapat diabaikan, i. e., aliran tidak viskos, kekekalan momentum linier direduksi menjadi persamaan Bernoulli yang terkenal. Tujuan dari contoh ini adalah untuk memahami peran hukum kekekalan dalam menentukan fisika aliran udara inkompresibel melalui nosel konvergen..
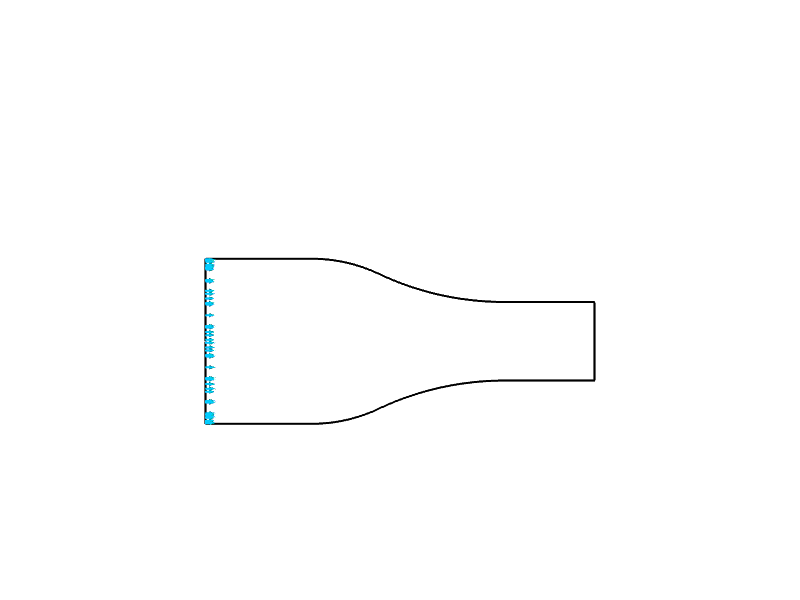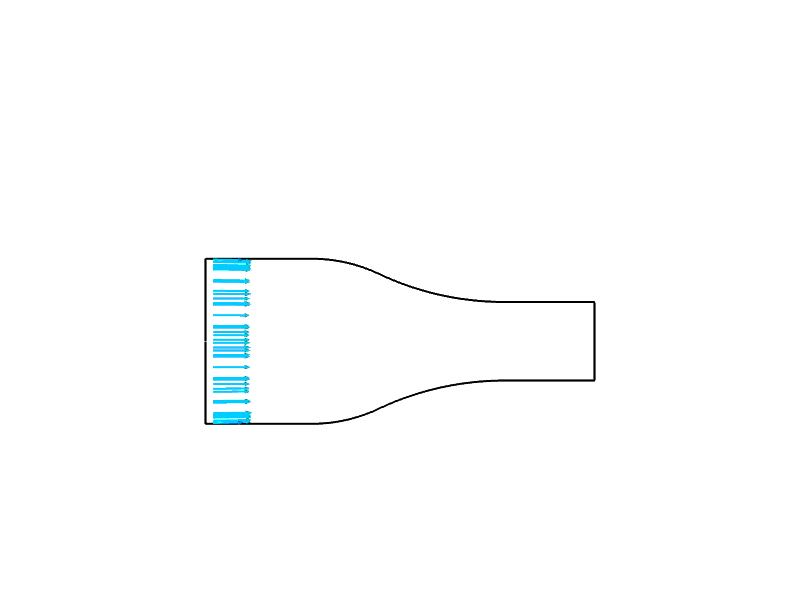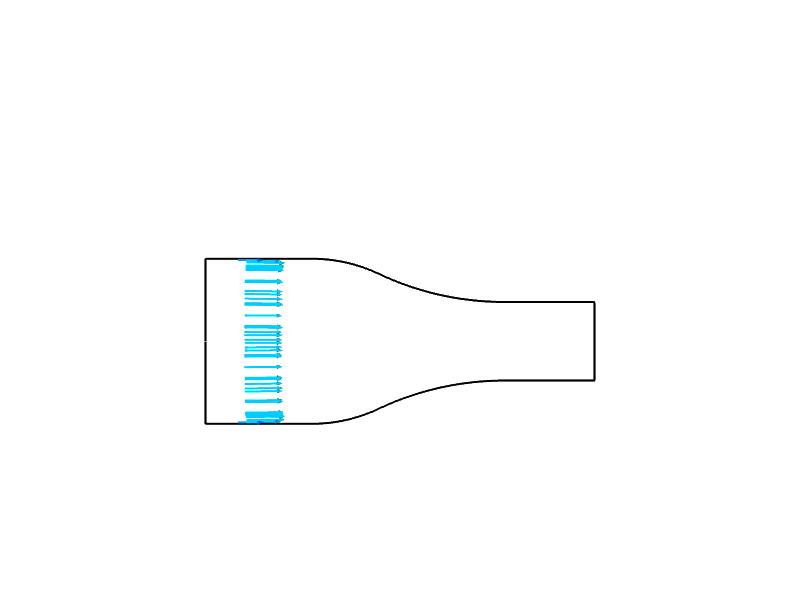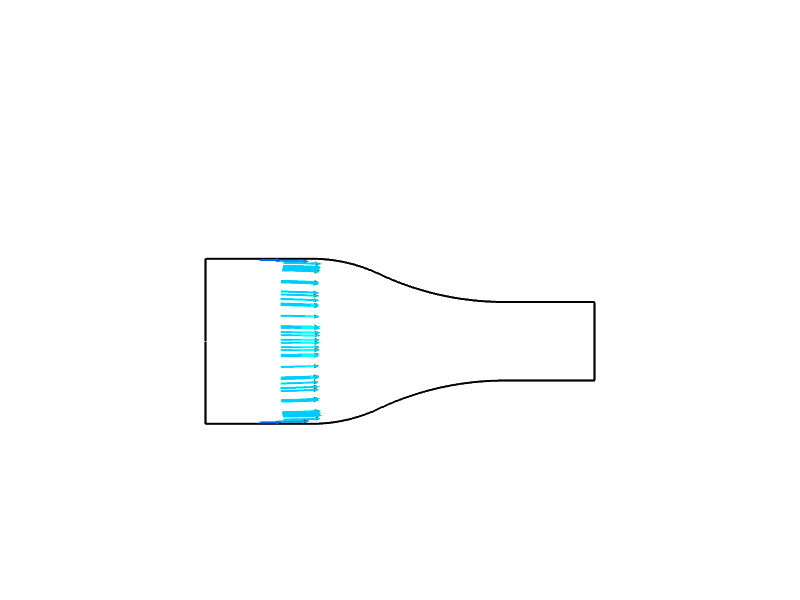
Tujuan
Dalam contoh ini, simulasi dilakukan untuk menghitung aliran udara melalui nosel konvergen. Anda akan mempelajari cara menyiapkan simulasi aksisimetri 2D dalam dua situasi: (1) dengan asumsi inviscid, dan (2) tanpa asumsi inviscid. Akhirnya, Anda akan memahami bagaimana menginterpretasikan hasil dari dua simulasi dengan membandingkannya dengan teori dan satu sama lain untuk mengidentifikasi perbedaan dan penyebabnya.
Setup
Unduh file Mesh yang diperlukan untuk menyiapkan simulasi dan file Kasus & Data terkait di sini. Ikuti petunjuk di bawah untuk menyiapkan simulasi ini di Ansys Fluent yang dimulai dengan file Mesh. Jika Anda menghadapi masalah saat menyiapkan atau menjalankan simulasi, lihat file Kasus dan Data awal dan akhir yang sesuai.
Hasil dan Diskusi
Mari kita menganalisis simulasi dan memahami fisika aliran udara yang tidak dapat dimampatkan melalui nosel konvergen.