Advent of Code

Advent of Code is an advent calendar of small programming puzzles made by Eric Wastl. Every day in December, it presents you with a small riddle, to be solved with code in the language of your choice.

In this article, we’re going to look at solving one of this year’s puzzles with Scade One.

“But wait!”, I hear you say. “Scade One is a specialized tool to create embedded software, surely you can’t solve general programming puzzles with it!”. Well I can, and I will, because the true magic of Christmas doesn’t only lie in writing code, but in making it run on impossibly constrained embedded hardware.

The rules

First, let’s lay down some ground rules. Scade One (and the underlying Swan programming language) is meant to create embedded software, that will run on various types of hardware, from multi-CPU boards to teeny tiny microcontrollers.

In a typical Scade One program, any interaction with the outside world (sensors, actuators or even a file system) typically happens through pre-allocated data structures. For this reason, it doesn’t really make sense to use Scade One to read and parse the raw text puzzle input from a file. Instead, we’ll be using a small Python Extract/Transform/Load script to turn the data into ready-to-use Swan types and constants.

Once we have the input data, though, all the logic will be implemented in Scade One.

Our problem

Our problem today is Day 3 of Advent of Code 2024.

Our program receives a character string as an input. Inside this character string are instructions that multiply some numbers. Well-formed multiplication instructions are written mul(a,b), a and b being 1-3 digit numbers.

Our program must:

• Compute the sum of all well-formed mul(a,b) instructions.
• Ignore badly-formed instructions, e.g. mul(2,2] or mul ( 4 , 6 ).

We are given an example string:

xmul(2,4)%&mul[3,7]!@^do_not_mul(5,5)+mul(32,64]then(mul(11,8)mul(8,5))

Well-formed mul(a,b) instructions are in bold above and add up to a total of 2*4 + 5*5 + 11*8 + 8*5 = 161.

Modeling a solution

So, we want to recognize patterns in a string. The right tool for this is a regular expression.

While we don’t have regular expressions out of the box in Scade One, we have something that does the exact same job: state machines. More precisely: safe, deterministic, memory-constant state machines.

Scade One programs use a dataflow paradigm. This means that we’re not describing step-by-step instructions, but rather describing the data and how it is transformed (via equations). The program runs in discrete time steps called cycles. At each cycle, the model transforms its inputs to outputs. The sequencing of operations is determined by the code generator, based on static analysis of the model. As far as the model designer is concerned, two independent, parallel operations happen simultaneously (this will be important later).

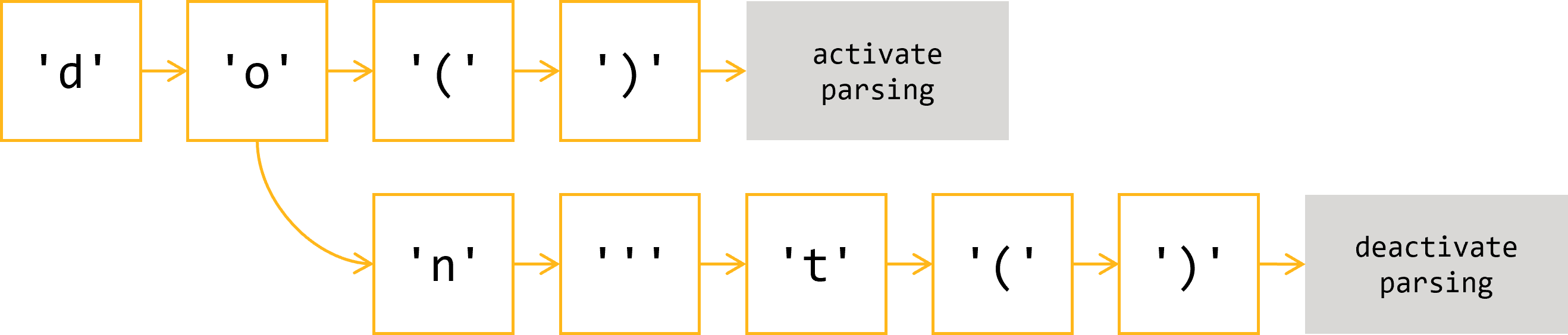
In our case, our Scade One model consumes a flow of characters, which is a sequence of char values that takes, at each cycle, the successive characters of our input string. We are looking for this progression:

At any point during this progression, if we find an unexpected character, we go back to the start. If we successfully make it to the closing parenthesis, we compute the multiplication and add it to a counter.

This is easy to translate into a Swan state machine:

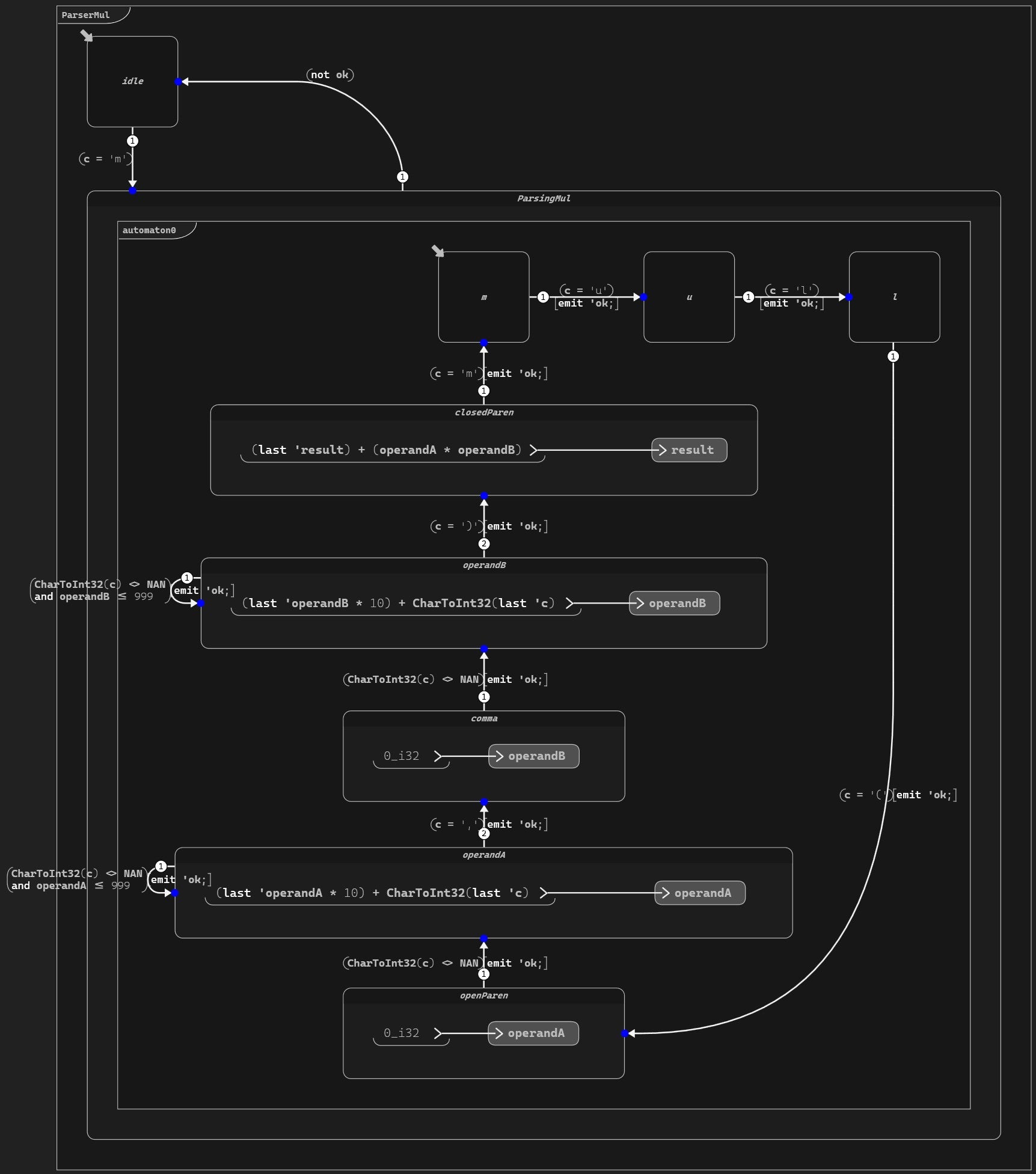
Our Swan state machine (click to enlarge)

Our state machine has two states: idle and parsingMul. When it’s parsing, it moves through the expected progression of characters, emitting a boolean ok flag to confirm that it should continue. Should an unexpected character be encountered, the ok flag is not emitted, and the state machine goes back to idle.

Furthermore, we maintain two variables local to the scope of the state machine: operandA and operandB, used to compute each multiplication and store them into result, the output.

One important thing to mention here: state machines are baked into the Swan language and work out-of-the-box. Their implementation is safe, deterministic, and operates at constant memory.

I don’t know about you, but my typical experience with state machines consists in either finding an obscure library and trying to use it correctly or implementing my own and spending more time debugging the state machine itself than my business logic. In my case at least, having safe and ready to go state machines is a relief.

Testing it out

Now that our state machine is complete, we need to test it. For this, we use a test harness, which is what Scade One calls its automated tests. Our harness is a special diagram that exercises the operator under test (outlined in purple below) and makes assertions on some values.

Let’s look at it in debug mode:

It works! You can see purple debug values that confirm our desired result of 161.

We can now apply our program to our (personalized and not posted here) ~20k character input string and successfully compute the correct answer.

Growing complexity

Each Advent of Code puzzle has a second part that brings some complexity to the initial problem. Here, in addition to mul(a,b) instructions, we must detect two new ones:

• do() enables future mul(a,b) instructions
• don't() disables future mul(a,b) instructions

Our program starts with mul instructions enabled.

We are given a new example string:

Xmul(2,4)&mul[3,7]!^don't()_mul(5,5)+mul(32,64](mul(11,8)undo()?mul(8,5))

Our program must detect the instructions in bold above. You can see that only two mul(a,b) instructions must be summed this time, for a total of 2*4 + 8*5 = 48.

Now, seeing as we already have a state machine, an immediate reaction may be to think about how we may make it more complex to handle this new logic. However, thanks to the synchronous nature of Scade One and to its dataflow paradigm, parallel processing is free; we can simply add another, simple state machine next to our existing one. Both state machines will execute in parallel, synchronously, and communicate using a boolean flag with no extra effort on our part.

Here’s the simplified version of our new state machine:

Here again, if we encounter an unexpected character at any part of this process, we simply go back to the start.

Here is our new state machine in Scade One:

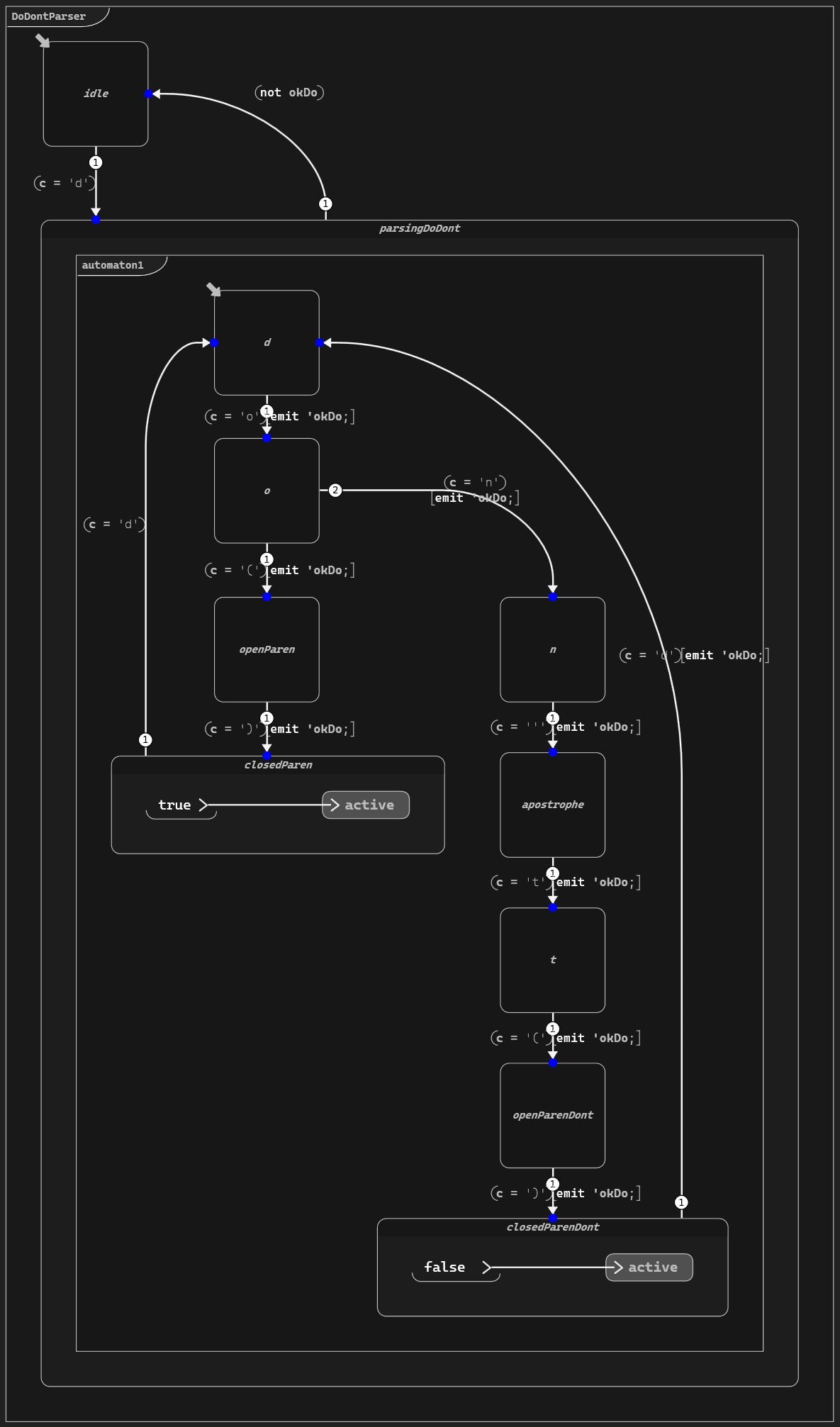
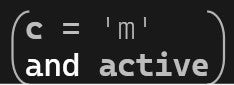
Our second state machine (click to enlarge)

This new state machine operates on the same principle as the previous one. Instead of integer operands, it maintains a boolean variable called active to determine whether mul expressions should be parsed. To use it in our first state machine, we simply expand the guard condition to detect our first m character:

Our first state machine using the active flag

Here is an animated view of our two state machines working together to process each character in the flow:

Our two state machines working together (click to enlarge)

We write a new test harness and confirm that our two state machines work together to find our desired result of 48:

Here again, we apply this new program to our long input string and successfully complete the puzzle! While we won’t post said string or result here (inputs are personalized and copyrighted), here is a cool visualization of our program running on the ~20k character string:

You can see that our result (yellow curve) grows steadily as parsing goes on and temporarily goes flat whenever our active flag (purple curve) is false.

We could have solved this with a regex

I know, right? And in some way, we did: our state machine above is exactly what a (compiled) regex would be doing to our flow of characters.

Let me add a few reasons why our approach may be desirable:

• If you plan on running your program on a tiny bare-metal device, you may not have a regex engine available (at least not one that fits the constraints of your hardware). With our state machine above, you are given a safe framework where you can predict, at compile time, exactly how much memory and processing power your program will need.
• If you’re doing MBSE, you may want to trace software requirements, or elements of your system architecture, to individual states / transitions of the state machine. This can’t be done with a fine granularity on a regex one-liner.
• If you’re building safety-critical software, you may want to avoid a dependency on a regex engine (that you’d then need to review as part of your safety certification). Having code with no external dependencies, that does exactly what you need and no more, saves effort at certification time.

Ready to take on the challenge?

In this article, we have seen how to use Swan state machines to process a flow of character data. We have seen that safe, deterministic, synchronous state machines are baked into the Swan language. We have also seen that parallel processing comes at no extra cognitive cost: side-by-side diagrams execute in parallel, and the code generator figures out execution order and dependencies for us.

If you’d like to play with the model presented in this article, you may download it here. You will need Scade One 2025 R1 or later to open it. If you are a SCADE user, access Scade One Essential with your existing licenses on the Ansys Download Portal.

You may also schedule a live demo of Scade One using this link.

And of course, if you’d like to give Advent of Code a shot, go to https://adventofcode.com/!

About the author