Learning Forum

[mdmech.mech]

Hello All,

I have modelled an oil-filled tank. It is subjected to a vibration of 25 mm/sec for a period of 2 seconds. I want to ensure that the designed component or parts are within the yield strength of the material. Can anyone suggest a procedure to perform the analysis? I don't know how to start this analysis. Some guidance would be very much appreciated.

[peteroznewman]

Let me re-state the vibration load.

• Peak velocity is 25 mm/sec for a sinusoidal ground motion.
• A period of 2 seconds is a frequency of 0.5 Hz.

You want to know the steady state response of the structure.

Let's put aside the fact that the tank is oil-filled for now because it makes the model slightly more complex and just focus on making a model to simulate the stress in an empty tank.

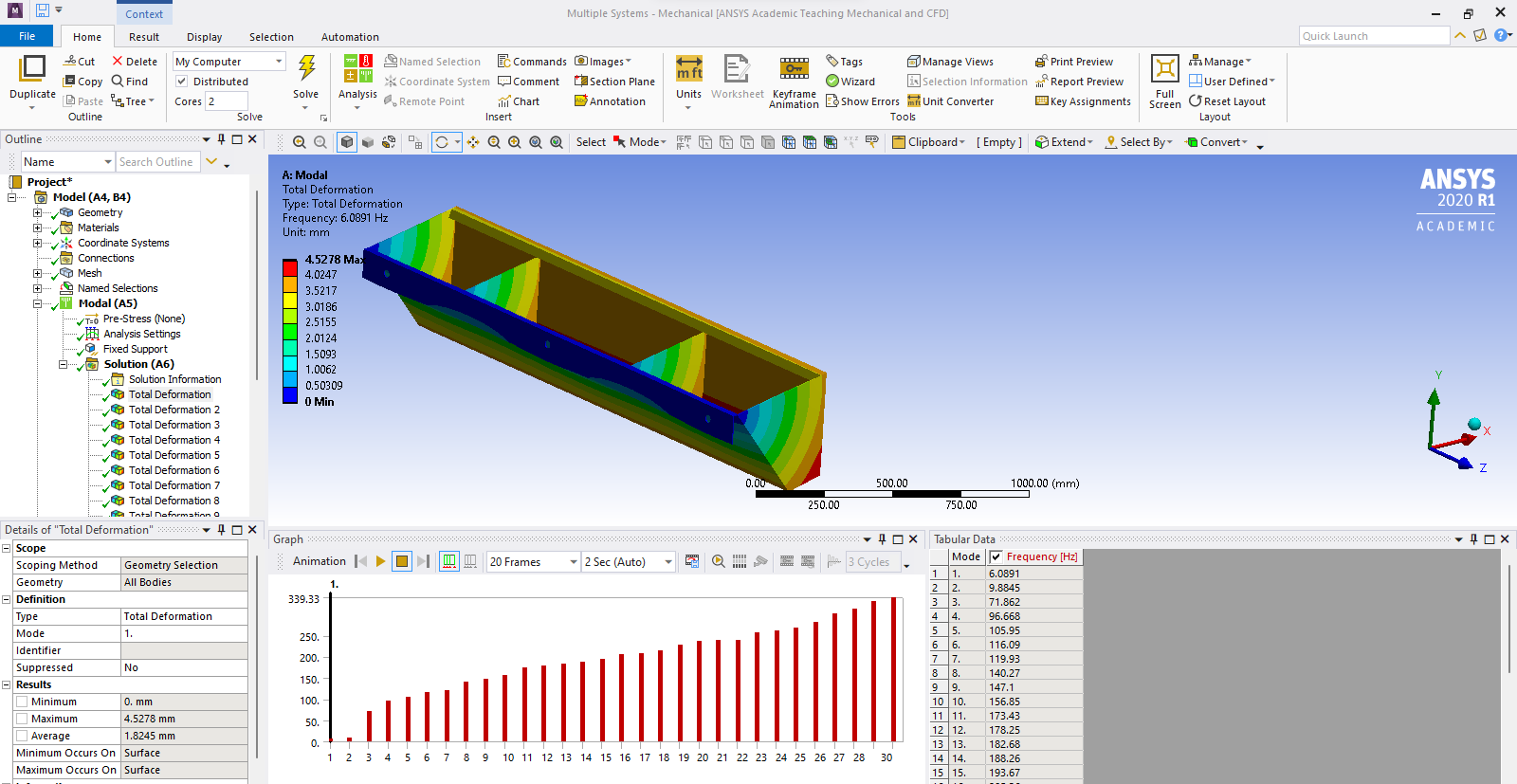
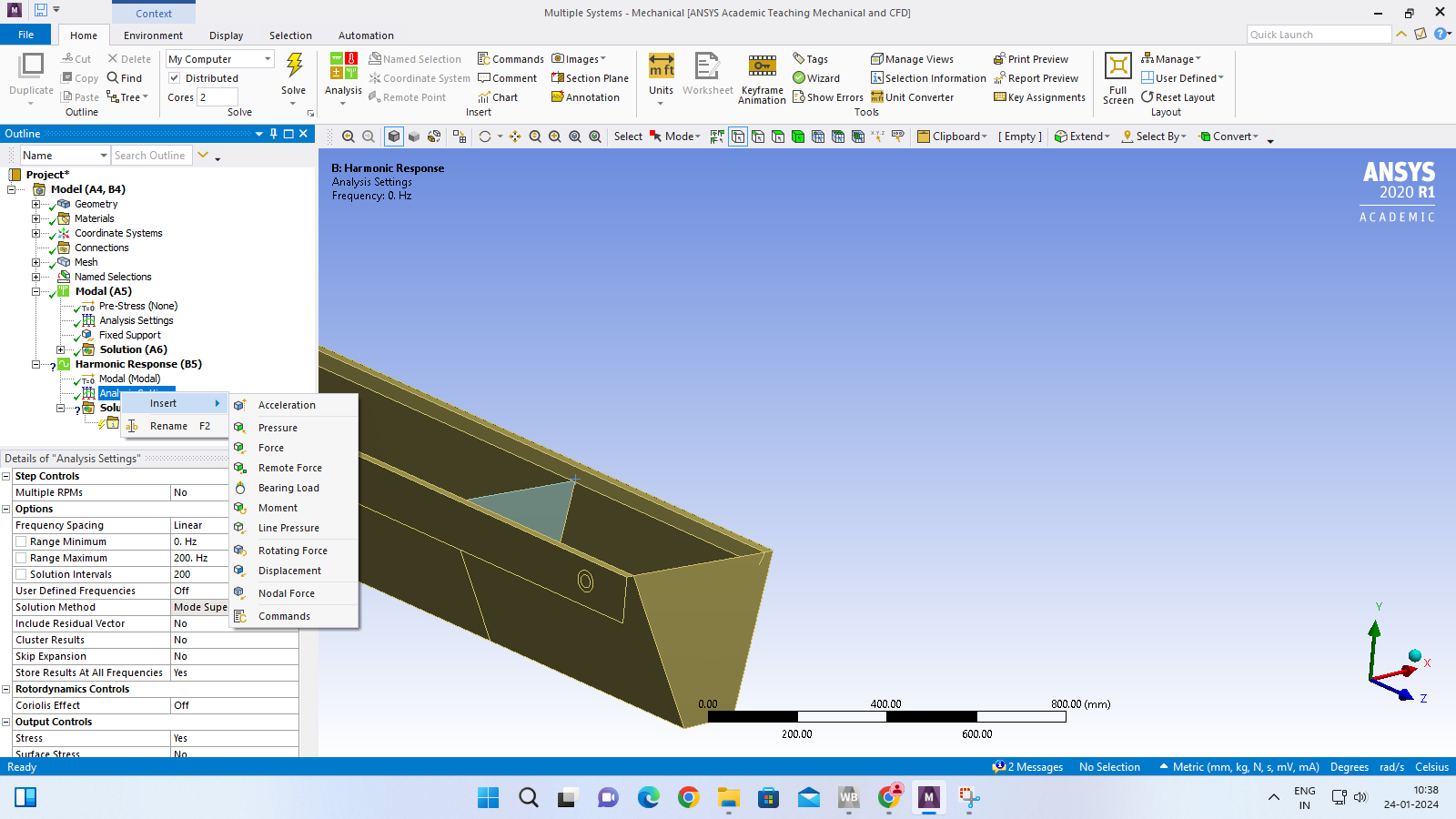
The analysis you want is called Harmonic Response.  It requires a Modal analysis to build upon.

Take the free courses on Harmonic Response and Modal then come back when you have attempted that for the empty tank.

/courses/index.php/courses/harmonic-response-analysis-in-ansys-mechanical/

/courses/index.php/courses/harmonic-analysis-of-structures/lessons/intro-to-harmonic-analysis-lesson-1/

/courses/index.php/courses/modal-analysis-in-ansys-mechanical/

[mdmech.mech]

Hi Peter,

As per your suggestion, i have completed the modal analysis course and the tank natural frequency extracted. While attempting to do the harmonic analysis followed by modal analysis, I could not able to insert the 25 mm/sec as a velocity for the frequency of 0.5 Hz. Can you please guide me for further process.

[peteroznewman]

Convert the velocity to acceleration by taking the derivative. The equation for the velocity is A*sin(w*t) where A is 25 mm/s and w is the circular frequency. Convert the 0.5 Hz frequency into a circular frequency. It's not important that the equation changes to a cos function. 

[mdmech.mech]

Thank you Peter,

velocity (A) = 0.025 m/sec, w = circular frequency is 3.14159 rad/sec, from this acceleration I have got is 0.2467 m/s^2. Am I correct? 

Mean while, how do I model the oil filled in the tank? Please suggest a procedure.

Thanks in advance

[peteroznewman]

How did you come up with that number? I don't think it is correct. 

Is the tank completely filled with fluid or is there a free surface with air or other gas at the top?

[mdmech.mech]

Hi Peter, From Internet, I have found a formula,

x = 0.025 m

acceleration = 4*π^2*f^2*x  = 0.2467 m/s^2

I am not sure, which method is correct

As you suggested,

f = 0.5 Hz

A = 0.025 m/s

w = 2*pi*f = 3.14159 rad/sec

velocity = A*sin(w*t)

t = 2 seconds

acceleration = A*w*sin(w*t) ---- As you said I have taken the derivative

                    = A*(2 * pi * f) * sin(w*t)

                     = 0.025*(2*3.1416*0.5)*sin(3.1416 * 2)

                     = 0.00859 m/s^2

Please give me a suggestion as to which value of acceleration I should take.

The tank is half filled with free surface with air at the top.

[peteroznewman]

The formula from the internet is to convert a displacement to acceleration. You have a velocity so you take the derivative of the velocity and you wrote a correct equation for acceleration.

The amplitude for the acceleration is A*w = 0.025*3.1416 = 0.07854 m/s^2.  Don't evaluate the sin(w*t) term, which you got wrong because you didn't use radians, but you only want the amplitude anyway.

I will reply later after I find a reference for adding the fluid to the tank. That question has been asked before so you can try searching for it also.