Learning Forum

[Emre Sakin]

Hello,

I am working on vibrations and modal analysis recently. I have a question that I could not find any answer. Can you please help me? 

Imagine a shaft. When we run the free free modal analysis lets assume that first bending mode is 600 Hz. Then we add 2 massless springs to the shaft. The first bending mode comes around 400 Hz. That means it decreased. How is it possible? If we add massless springs does not that mean the stiffness will increase? Can you please explain with formulas or send me some articles or books to understand it better.

Many thanks in advance.

Best regards.

[Zoi Stavrothanasi]

Hello Emre,

 

It is true that, when massless springs are added to a model, commonly they contribute additional stiffness to the system. This increase in stiffness generally leads to higher natural frequencies. However, it is worth noting, that except friquency, other factors such as changes in mass distribution, boundary conditions, or damping effects can also influence the natural frequencies of the structure. 

 

You can find more detailed information about spring elements (COMBIN14, COMBIN39, COMBIN40) used in modal analyses in Ansys element librady.

 

Moreover, in the context of modal analysis, the eigenvalue problem is used to determine the natural frequencies and mode shapes of a vibrating system. For a clearer understanding of the concept, you may find the ”An Eigenvalue Problem — Lesson 3” video from Ansys Learning informative.

 

Hope these help!

[Emre Sakin]

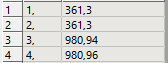
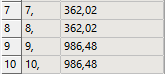
Thank you for the answer. To be more clear I have uploaded some images. I draw a shaft. When I run free free modal analysis first bending mode is 362,2 and second bending mode is 986,45 but when i fix the shaft from 2 sides the first bending mode decreases to 361,3 and the second to 980,9. What is the reason for that? 

fixed supports

pinned modes

free modes

Thank you.

 

 

[Zoi Stavrothanasi]

“Free-free” indicates that the structure is free of load and free of boundary conditions. So, the structure is free to have rigid movement in 6 degrees of freedom in three-dimensional space. Free – free modal analyses are used to find the natural frequencies of the unconstraint model.

When adding fixed supports to a model, the modes represent the vibration modes of the structure under specific boundary conditions. Thus, the fixed boundary conditions can influence the distribution of mass and stiffness and alter the resulting modes compared to the free modal analysis.

[Emre Sakin]

Thank you for the answer. I have one more question. I run another analysis which has pinned-pinned boundry conditions from the top and the bottom faces. And I saw that first bending mode was 160 Hz. Why did it decrease that much? 

Thank you in advance.

[Zoi Stavrothanasi]

Hello Emre,

By adding pinned supports, the rotational movement of the shaft at the ends is restricted, affecting the bending behavior. These supports, are providing extra resistance against bending moments comparing to the free-free support and reducing the magnitude of the bending modes.

Hope these help!