TAGGED: circular-polarization, polarization
-
-
September 7, 2023 at 6:50 am
xuanlunhuang20
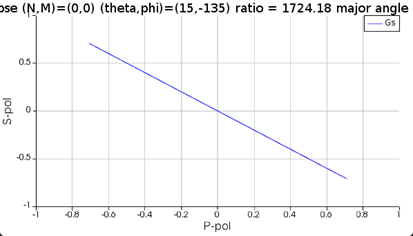
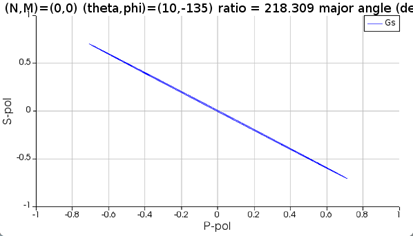
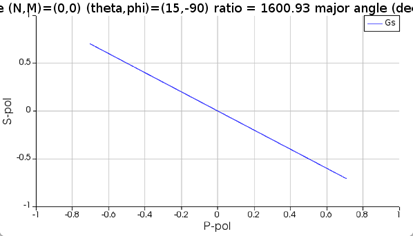
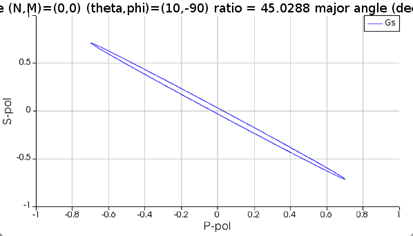
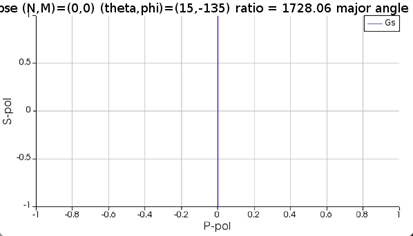
SubscriberI designed a quarter waveplate and I used a circular polarized source to test whether it could transform the source back to a linear polarized light. I tried to plot the far-field polarization ellipse and analyzed the result. However, I met a problem when I set the theta angle and the phi angle to be 15 degrees and 45 degrees, respectively. The far-field polarization ellipse passed through this quarter waveplate is different from that of the source. I also tried other settings of angles, which are shown at the end of this post. From these settings, it seems that the passing light can be transformed back to the direction of the original source except in this setting “theta=15 and phi=45”.
How should I understand these polarization ellipses and why does the result of the case “theta=15 and phi=45” look like this?
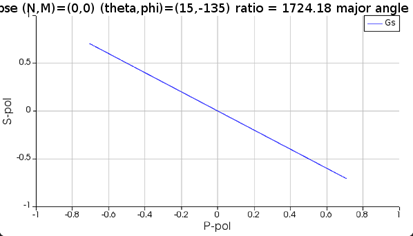
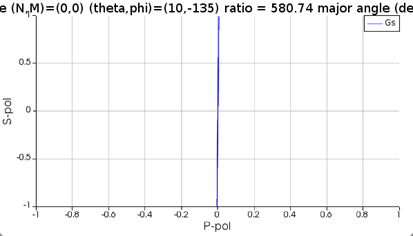
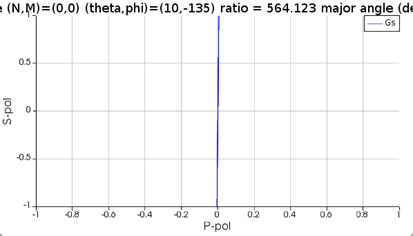
As you can see from the following two results, if I set the phase difference between two sources to be 0, the polarized light is 45 degrees, while the circularly polarized light is transformed to 90 degrees polarized light after passing through the waveplate.
(1) Source1:theta=15,phi=45,pol=0,phase=0; Source2:theta=15,phi=45,pol=90,phase=0
(2) Source1:theta=15,phi=45,pol=0,phase=0; Source2:theta=15,phi=45,pol=90,phase=90
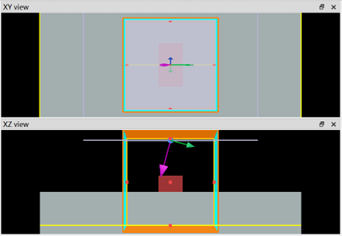
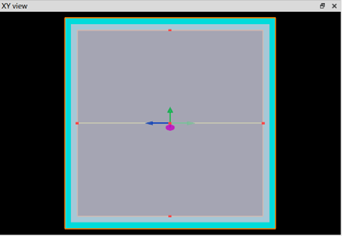
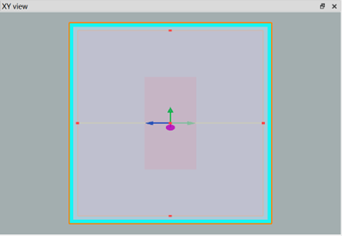
The structure is shown in the following pictures. The material of the meta-atom is “Si (Silicon) – Palik”, and that of the substrate is “SiO2 (Glass) – Palik”. The working wavelength is 850nm and the propagation direction is backward. The structure size of the meta-atom is 100nm in x width, 178nm in y width, 485nm in height, and 357nm in period.
Some other tests:
(1)Because the vector sum of two sources is along the y direction of the meta-atom, it only adds a global phase to the source. The direction of the polarization remains the same as that of the source.
Source1:theta=15,phi=45,pol=0,phase=0; Source2:theta=15,phi=45,pol=90,phase=0
Source1:theta=15,phi=45,pol=0,phase=0; Source2:theta=15,phi=45,pol=90,phase=0
(2)Because the vector sum of two sources is 45 degrees to the y direction, the circularly polarized light (ssource1 phase=0, ssource2 phase=90) is transformed back to a linear polarized light, whose direction is the same as that of a linear source (source1 phase=0, ssource2 phase=0).
Source1:theta=15,phi=90,pol=0,phase=0; Source2:theta=15,phi=90,pol=90,phase=0
Source1:theta=15,phi=90,pol=0,phase=0; Source2:theta=15,phi=90,pol=90,phase=90
(3)Because the vector sum of two sources is 45 degrees to the y direction, the circularly polarized light (ssource1 phase=0, ssource2 phase=90) is transformed back to a linear polarized light, whose direction is the same as that of a linear source (source1 phase=0, ssource2 phase=0).
Source1:theta=15,phi=45,pol=45,phase=0; Source2:theta=15,phi=45,pol=135,phase=0
Source1:theta=15,phi=45,pol=45,phase=0; Source2:theta=15,phi=45,pol=135,phase=90
-
September 7, 2023 at 10:59 pm
Guilin Sun
Ansys Employee"The far-field polarization ellipse passed through this quarter waveplate is different from that of the source"
Isn't this expected? you used a circular polarized source, and after the waveplate it changes to linearly poolarized light as it shuld be. right? do you expect to be the same as the source circular polarization? from your description I am confused.
A1: you get the linear polarization with linear polarized sources. seems without waveplate, right?
A2: the vertical line in the polarization plot means it is a linear polarization but not 45 deg linearly polarization.
I think your results are correct but you need to uderstand them, for example what the theta, phi mean in the plot? what is the difference between phi=-135 and phi=-90?
You already got the linearly polarized results, Then you need to correctly interpret them.
-
September 8, 2023 at 3:13 am
xuanlunhuang20
SubscriberSorry for the unclear expression. For example, I set the phase difference between two sources to be 0 degree, the vector sum is a linearly polarized light, right? Then I simulate without the waveplate structure, I can get a polarization plot of the linearly polarized light. Next, I set the phase difference to be 90 degree, it is a circularly polarized light. After passing through the quarter waveplate, this “90 degree” phase difference should be eliminated and the circularly polarized light can be converted back to the linearly polarized light. Hence, I am expecting that if I use a circularly polarized light to pass through the waveplate, the direction of output polarization plot should be the same as that of the linearly polarized light. However, it’s not the case for the situation “theta=15 and phi=45”.
In “some other tests“, I wanted to verify my expecting and used three cases to test. It seems that in these three cases, the output polarization plot of the waveplate is the same as that of the original linear polarized light which is simulated without the waveplate.
For case (1), I first got the polarization plot of a linearly polarized light, which was simulated without the structure. Next I enabled the waveplate structure and used the same linearly polarized light to simulate. Because the vector sum of this linearly polarized light is along the y direction of the meta atom, it will not be transformed to a circularly polarized light. So the output polarization is the same as that of the original source which is simulated without the structure. This accords with intuition.
For case (2), I got the polarization plot of a linearly polarized light first. Next I changed the phase between two sources to be 90 deg to create a circularly polarized light. Because the vector sum of E field is 45 deg to the y direction, the waveplate should work. Therefore, after passing through the waveplate, this circularly polarized light was converted back to the original linearly polarized light. The output polarization plot is similar to the original linearly polarized light, this is also what I expect.
For case (3), similar to case (2), the vector sum of E field is also 45 deg to the y direction. Therefore, after passing through the waveplate, the circularly polarized light can be converted back to the original linearly polarized light. The output polarization plot is also similar to the original linearly polarized light.
However, for the case “theta=15 and phi=45”, the polarization plot of the linearly polarized light without the structure is in 45 degrees while the circularly polarized light is transformed to vertical direction after passing through the waveplate. I know the function of the quarter waveplate is correct, I just wonder why the case “theta=15 and phi=45” is different from the others.
-
-
September 8, 2023 at 5:44 pm
Guilin Sun
Ansys Employee"However, for the case “theta=15 and phi=45”, the polarization plot of the linearly polarized light without the structure is in 45 degrees while the circularly polarized light is transformed to vertical direction after passing through the waveplate. I know the function of the quarter waveplate is correct, I just wonder why the case “theta=15 and phi=45” is different from the others."
I guess the confusion is from phi. When phi is not zero, the polarization actually changes. Please check! When phi=0 but theta is non zero, the polarization is still in the plane, say xz. However if phi is not zero (theta is also not zero), then the polarization is not only in xz plane, but also in yz plane.
If phi=0, the polarization is at 45 deg after the waveplate with circular polarization. When phi is 45, the result changed to 90 deg, which is correct. It will not be 45 deg.
Please check the polarization state:
1: linear polarization of theta 15deg, phi=0;
2: linear polarization of theta 15 deg but phi=45.
The textbook gives simple case for illustation. Now you are working on a complicated case so you may need to follow the first principle and see where the polarization should be when phi is not zero.
I believe your simulaiton results are correct.
-
September 9, 2023 at 12:32 pm
xuanlunhuang20
Subscriber"If phi=0, the polarization is at 45 deg after the waveplate with circular polarization. When phi is 45, the result changed to 90 deg, which is correct. It will not be 45 deg. "
This is really a way to understand this problem. Thank you.
Next, I will simulate more cases to see whether I can come to a summary.
-
-
- The topic ‘Issue in plotting the farfield polarization ellipse for a quarter waveplate’ is closed to new replies.



-
3467
-
1057
-
1051
-
929
-
896

© 2025 Copyright ANSYS, Inc. All rights reserved.