Learning Forum

[josegegas]

Hello. When one performs a transient simulation, joint force and torque must be distributed among the fem nodes belonging to the bearing face. I was wondering if user has any control over how this distribution takes place? I am trying to simulate a simple flexible pendulum but I do not get correct answers because Ansys seems to apply the joint force to the wrong face nodes using the default configurations at least.

Any help will be welcome. Thanks

[peteroznewman]

Please reply with more details. What kind of joint?  What kind of elements (solid, shell, beam)?  What is the shape of the bearing face?  What is the correct answer and where did that come from?

[josegegas]

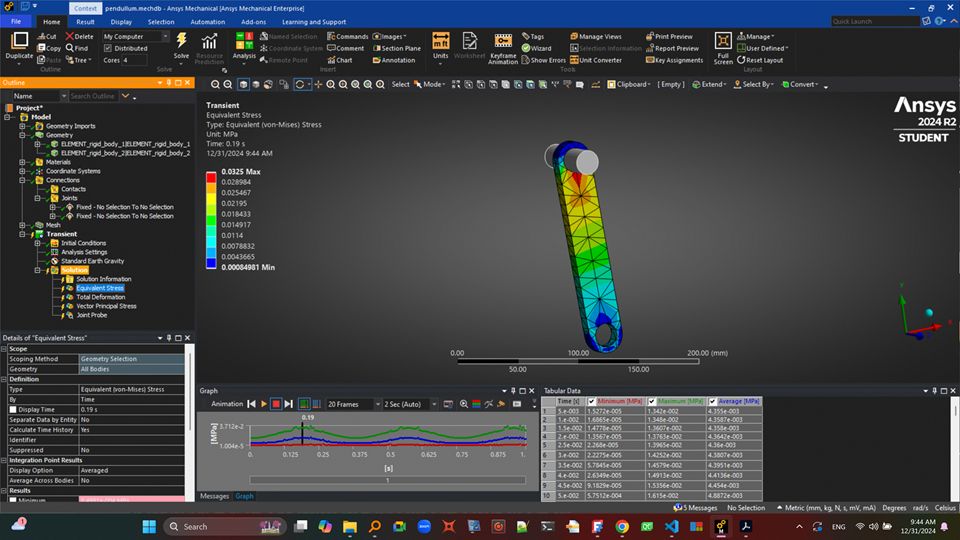
Here is an image. There are two joints: A fixed joint grounds the pin, and a revolute joint connects the pin and the pendulum (although, I do not know why; Ansys shows the second joint label as "fixed", but it is in fact a revolute). I set Earth's gravity pointing to global -Y. The pendulum is initially at the horizontal position, aligned with global X. The hinge axis is parallel to global Z, so the pendulum swings along the X-Y plane. When the pendulum swings, the revolute joint sees a reaction force. I have verified the value of this force by using another software to perform the same simulation and coparing the forces with those computed by Ansys. Reaction forces are correct. The bearing face is the cylindrical inner face of the pendulum hole, around which it pivots. I have removed the contacts Ansys adds bu default. I use solid tetrahedron elements for the mesh. I want to see the stresses in the pendulum resulting from the swinging. For this, Ansys should distribute the revoute joint force among the nodes that belong to the bearing face, and of course include the inertial forces resulting from the swinging in the fem simulation. But the thing is that the result stress distribution does not make sense. In the image above you can see von-Mises stress when the pendulum is near its vertical position (when the joint force is maximun and points to global +Y). You can see stress is concentrated at the bottom of the hole, which does not make sense: it must be at the top and in the sides instead. I believe this is because Ansys is distributing the joint force among the nodes in the bottom half of the hole instead of in the top, but Im not sure about this. So I would like to know how Ansys distributes rigid joint loads into the fem nodes, and If I have any control over how loads are distributed? 

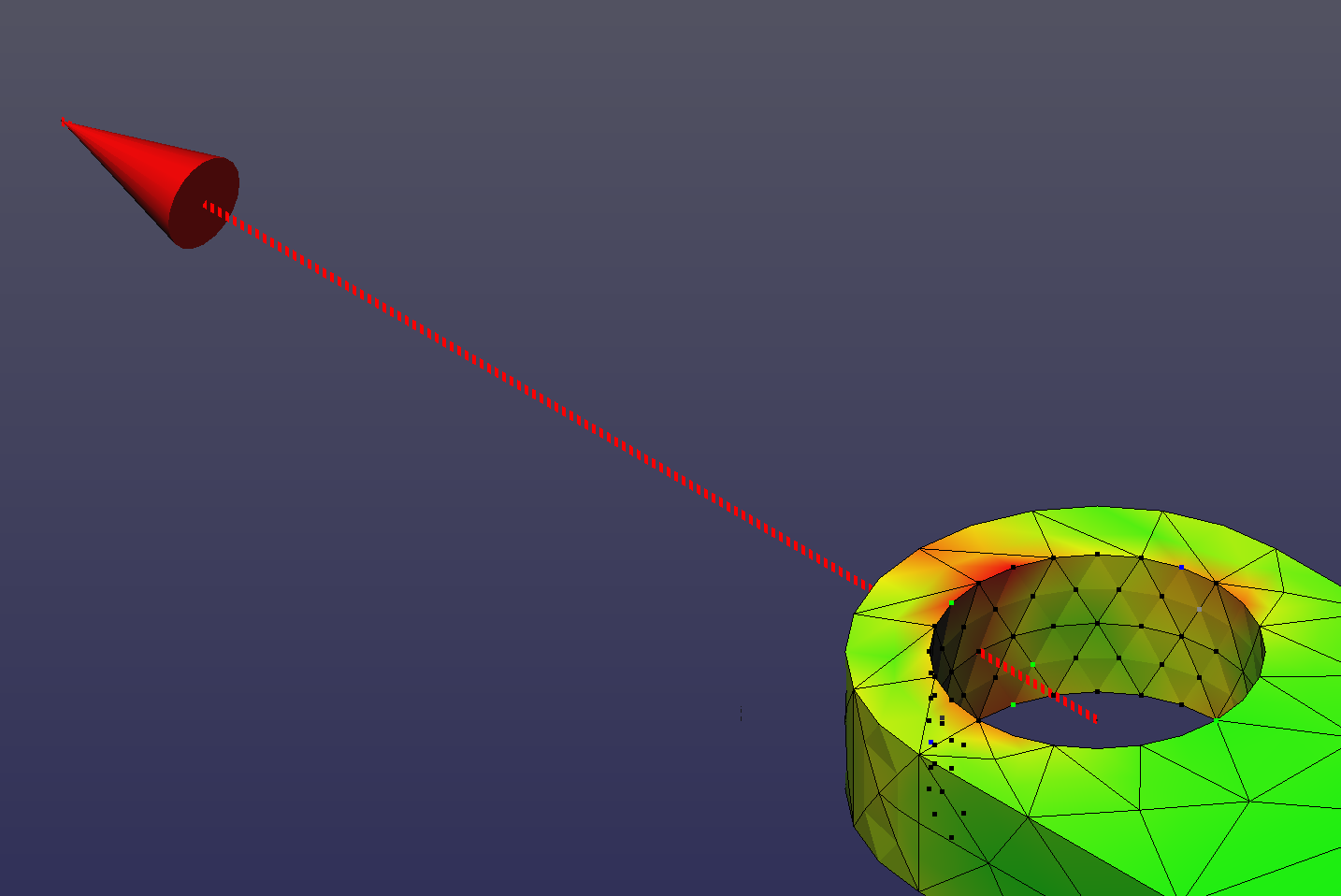
Here is a picture of what I am convinced is the correct stress distribution, simulated using another software.The red arrow is the joint force when the pendulum is vertical (half of its oscillation). The force computed by Ansys is correct: it is the same as the red force vector shown above and calculated with the other program. You can see that here the stress distribution is different than in Ansys results, and this stress distribution makes sense considering the force that the pin puts on the bearing face of the pendulum. In this image you can also see highlited the nodes among which the joint force (red vector) is distributed. These are only half of the nodes in the bearing face: in real world the pin would exert force only among these nodes. So given that Ansys is computing the correct joint force I think the problem is that it may not be distributing this force correctly among the nodes? I used exactly the same geometry for both simulations, same CAD, same density, same Young modulus and Poison's ratio, and verified mass and inertia matrix are good in both cases. Here is a video for reference. The first is Ansys and the second is the other software:

https://www.youtube.com/watch?v=8q90GKWCilQ

 

[peteroznewman]

A revolute joint idealizes a pin-hole connection between two bodies to make transient structural models solve much faster while delivering accurate forces. The trade-off for the fast solve is the local bearing stress is not accurate.  There are several ways to obtain more accurate stress near the hole where the pin presses on one side of the hole.

A quick and simple way to improve the accuracy of the stress near the hole is to duplicate the transient structural model of system A to create system B, then replace B with a Static Structural analysis. Suppress the pin and joints, leaving only the link with two holes. Make the far hole a Fixed Support and apply the peak force over time from analysis A as a bearing load on the hole in analysis B, acting along the length of the link. A bearing load will create a good representation of the radial distribution of forces on the hole that add up to the total axial force. You will see the largest force at the top of the hole and the force will reduce to zero at +/- 90 degrees on either side. One advantage of this method is you can have a much more refined mesh because you only have to solve it once. The next method requires the solution to be completed for each time step, so a refined mesh takes much longer to solve.

A more accurate result for the stress near the hole is to delete the revolute joint and replace it with Frictional Contact between the pin and the hole. You might need additional axial contacts to prevent the link sliding off the pin, or the simulation might run without that.  The trade-off for the more accurate stress is it will take much longer to solve. Frictional contact is slightly more accurate than the bearing load because the deformation of the hole can only be to match the cylindrical shape of the pin.  The bearing load mentioned above does not limit the deformation to follow the surface of the pin, because there is no pin. If the wall thickness around the end of the hole was very thin, then that thin section could deform into a non-cylindrical shape under the varying radial bearing load.

[josegegas]

 

 

I would not say stress is “not accurate” in the Ansys simulation results above. “Not accurate” impies at least some accuracy, but to me in this case the stress distribution is plain wrong. Ansys is showing minimum stress in the areas where in reality there would be maximum stress and vice-versa. 

I also think a static structural analysis as descrived would not solve the issue. There will be some problems with this approach. First, a fixed support at one end would show stresses around the fixed nodes or even in other areas of the part, stresses that do not exists in reality. Second, the peak load at the other end may not be correctly distributed among the nodes in the bearing face. The load distribution may not be an accurate representation of how the pin would in reality apply load to the pendulum. This of course depends on the algorithm Ansys uses to distribute load using the “bearing load”. Is there a destription of this algorithm? Another issue with this is that the joint may also exert torque in addition to force. This torque woud have to be applied as a load to the bearing nodes, but how?

I think Ansys may have a better way to do this. Something like what other solvers call “inertia relief”. “Inertia relief” may also be a good description of how the results were obtained with the other software mentioned above. It basically computes the inertial forces for each solid element in the mesh, for each time-step of the MbD simulation, and then does the fem cancelling-out these inertial forces, by applying the “d’Alembert” force to each element. Taken from Wikipedia: “D’Alembert showed that one can transform an accelerating rigid body into an equivalent static system by adding the so-called “inertial force” and “inertial torque” or moment..”

How to do this in Ansys? How to apply “inertia relief”? I assumed Ansys would do this by default when doing transient analysis. 

 

 

[peteroznewman]

 

When you know how a revolute joint connection works, then you know to ignore the stress for a few diameters around the hole. Yes, it is plain wrong on the surface of the hole since it applies tension forces on the opposite side of the hole to the true solution, but this is fine if you know that and are willing to accept the trade-off to get accurate forces in a short amount of time. Remember that Saint-Venant’s principle tells us that the difference in stress in the link a large distance from the hole will become very small, even when the stress at the hole surface is just plain wrong.

In the simple Static Structural analysis I suggested, stress at the hole becomes fairly accurate, with the trade-off that the stress at the other end has become just plain wrong. But this is fine if you know that and ignore the stress at the other end. The bearing load applies forces in the radial direction only with a cosine fall off. Nodes have a force weighting of cosine(angle) between 0 and +/-90 degrees and the sum of the forces in the chosen direction equal the assigned value. As I mentioned, a bearing load is a good approximation for the load distribution of a close fitting pin in a hole and has the benefit of being quick and easy to use. I described the most accurate method of calculating stress in the hole and you are welcome to use that when needed but know that it will take more time.  In many cases, the extra time is not warranted.

There are several methods to get accurate stress near the hole.  A third method is to use Inertia Relief, which is available in Ansys. It will also use the Bearing Load in a Static Structural analysis so will give the same stress around the hole as the Static Structural analysis with the Bearing Load and the Fixed Support, but will not produce the wrong stress at the fixed support end. Click on Analysis Settings to turn Inertia Relief On. Watch this video for more information on Inertia Relief.