Learning Forum

[Vijay Adhi]

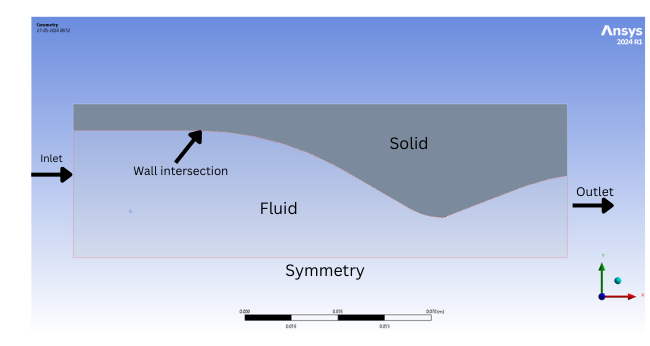
I'm working on the design of a pressure-fed LO2 and LNG rocket engine. I've been using Fluent to estimate the heat flux for an ablative-cooled engine. I was able to solve all the compilation errors for my UDF.

I'm attaching my boundary conditions and mesh. My model is axisymmetric and I have a fluid-solid domain in my problem, so all my methods are second order. But I keep getting this error whenever I run my calculations.

"Divergence detected in AMG solver. temporarily reducing Courant number to 0.5 and trying again..."

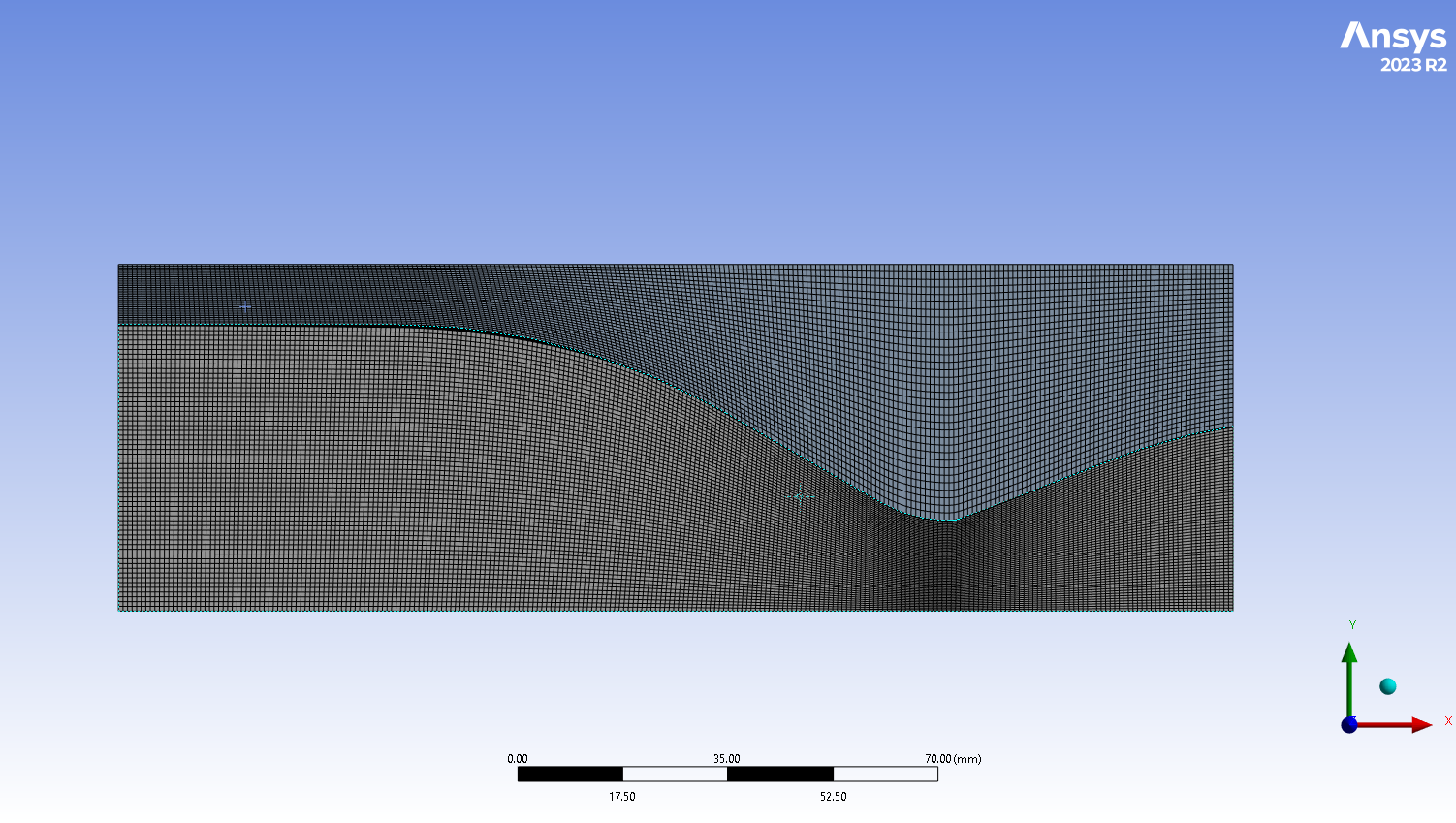
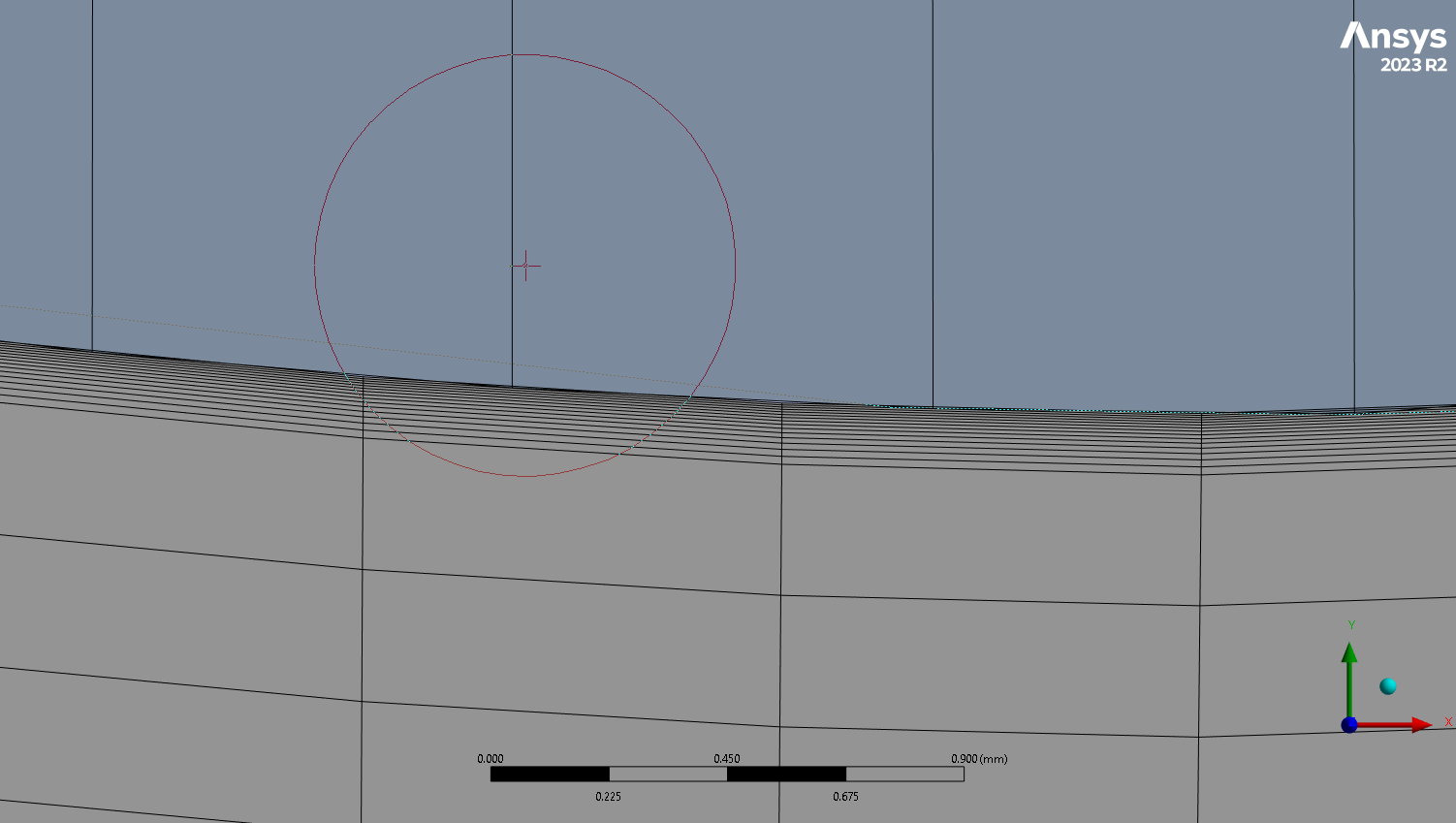
Is there a problem with my mesh? I've used a multi-zone and face mesh with 15 inflation layers.
I've tried all the methods I know to simplify the problem, my mesh quality is fairly good. I still keep getting the same error

(The actual mesh is much more refined, the picture quality is quite poor)

I'm attaching my UDF below:

#include "udf.h"

#define pi 3.14159

 

DEFINE_PROFILE(Boun_cond,t,i)

 

{

 

real x[ND_ND];

 

real rt, dt, At, vis, Cp, Pr, Pc, Tc, gamma, Cstar,Cstareff, g, r, A, M, Mnew, N1, N2, N3, Taw, Thotgas,T,hgas,func, ffunc, fCO2, fH2O, Le, qrad, qCO2, qH2O, P, mdot,kt;

 

face_t f;

 

int k,NI;

 

rt=0.015085; /* m        */

vis=0.000075018; /*Kg/m-s    */

Cp=2328.6; /*J/Kg-K    */

Pr=0.6552;

Pc=2500000; /*Pa */

Tc=3235; /*K */

gamma=1.20;

Cstar=1855.4; /*m/s */

Cstareff = 0.92;

kt = 0.2662; /*W/mK */

 

NI=1000;

 

dt=rt*2;

At=pi*pow(rt,2);

 

fCO2=0.10511; /*Mole fraction of CO2 */

fH2O=0.46300; /*Mole fraction of H2O */

mdot = 0.987; /*Mass flow rate of exhaust */

 

begin_f_loop(f,t)

 

{

 

F_CENTROID(x,f,t);

r=sqrt(pow(x[0],2)+pow(x[1],2));

A=pi*pow(r,2);

Le=0.6*2*r;

 

/*For combustion chamber */

 

if (x[0]<0.06604)

 

{

 

M=0;

P=Pc/pow((1+(gamma-1)*pow(M,2)/2),(gamma/(gamma-1)));

T=Tc/(1+(gamma-1)/2*pow(M,2));

Taw=Tc*((1+pow(Pr,0.33)*((gamma-1)/2)*pow(M,2))/(1+((gamma-1)/2)*pow(M,2)));

Thotgas=T+0.9*(Tc*pow(Cstareff,2)-T);

hgas=0.01975*pow(k,0.18)*pow((mdot*Cp),0.82)/pow((2*r),1.82)*pow((Thotgas/(F_T(f,t))),0.35);

 

/*Radiation heat transfer              */

 

qCO2 = 5.74*pow((P*fCO2*r/(pow(10,5))),0.3)*pow((F_T(f,t)/100),3.5);

qH2O = 4*pow((P*fH2O*r/(pow(10,5))),0.3)*pow((F_T(f,t)/100),3.5);

 

qrad=qCO2+qH2O;

 

}

 

 

/*For subsonic region                   */

 

if (x[0]<0 && x[0]>=0.06604)

 

{

 

for (k=1;k<=NI;k++)

{

if (k==1)

M=0.05;

else

M=Mnew;

 

N1=2/(gamma+1);

N2=(gamma+1)/(2*(gamma-1));

N3=1+(gamma-1)*pow(M,2)/2;

 

func = pow(N1, N2) * pow(N3, N2) / M - A / At;

ffunc=-pow(N1,N2)*pow(N3,N2)*pow(M,-2)+pow(N1,N2)*N2*pow(N3,N2-1)*(gamma-1);

 

Mnew=M-func/ffunc;

if(fabs(Mnew-M)<0.01)

break;

}

 

P=Pc/pow((1+(gamma-1)*pow(M,2)/2),(gamma/(gamma-1)));

T=Tc/(1+(gamma-1)/2*pow(M,2));

Taw=Tc*((1+pow(Pr,0.33)*((gamma-1)/2)*pow(M,2))/(1+((gamma-1)/2)*pow(M,2)));

Thotgas=T+0.9*(Tc*pow(Cstareff,2)-T);

hgas=0.01975*pow(k,0.18)*pow((mdot*Cp),0.82)/pow((2*r),1.82)*pow((Thotgas/(F_T(f,t))),0.35);

 

/*Radiation heat transfer              */

 

qCO2 = 5.74*pow((P*fCO2*r/(pow(10,5))),0.3)*pow((F_T(f,t)/100),3.5);

qH2O = 4*pow((P*fH2O*r/(pow(10,5))),0.3)*pow((F_T(f,t)/100),3.5);

 

qrad=qCO2+qH2O;

 

}

 

 

/*For Supersonic region*/

 

if (x[0]>=0)

 

{

 

for (k=1;k<=NI;k++)

{

if (k==1)

M=5;

else

M=Mnew;

 

N1=2/(gamma+1);

N2=(gamma+1)/(2*(gamma-1));

N3=1+(gamma-1)*pow(M,2)/2;

 

func = pow(N1, N2) * pow(N3, N2) / M - A / At;

ffunc=-pow(N1,N2)*pow(N3,N2)*pow(M,-2)+pow(N1,N2)*N2*pow(N3,N2-1)*(gamma-1);

 

Mnew=M-func/ffunc;

if(fabs(Mnew-M)<0.01)

break;

}

 

P=Pc/pow((1+(gamma-1)*pow(M,2)/2),(gamma/(gamma-1)));

T=Tc/(1+(gamma-1)/2*pow(M,2));

Taw=Tc*((1+pow(Pr,0.33)*((gamma-1)/2)*pow(M,2))/(1+((gamma-1)/2)*pow(M,2)));

Thotgas=T+0.9*(Tc*pow(Cstareff,2)-T);

hgas=0.01975*pow(k,0.18)*pow((mdot*Cp),0.82)/pow((2*r),1.82)*pow((Thotgas/(F_T(f,t))),0.35);

 

/*Radiation heat transfer              */

 

qCO2 = 5.74*pow((P*fCO2*r/(pow(10,5))),0.3)*pow((F_T(f,t)/100),3.5);

qH2O = 4*pow((P*fH2O*r/(pow(10,5))),0.3)*pow((F_T(f,t)/100),3.5);

 

qrad=qCO2+qH2O;

 

}

 

F_PROFILE(f,t,i)=(hgas*(Taw-F_T(f,t))+qrad);

}

 

end_f_loop(f,t)

 

}

 

 

 

 

 

[Rob]

Check the IF statements and that the various equations return a sensible value for all conditions.