-
-
April 19, 2021 at 3:46 pm
noumanzia
SubscriberHi,nHow can I code a bend in Lumerical such that its two endpoints are always at the fixed location when the bend radius is changed. So far I think that it can be done through polygon with circle equation because ring structure in Lumerical varies the endpoints when the radius is changednBelow is my schematic for the waveguide where I want to fix a curve between points A and Bn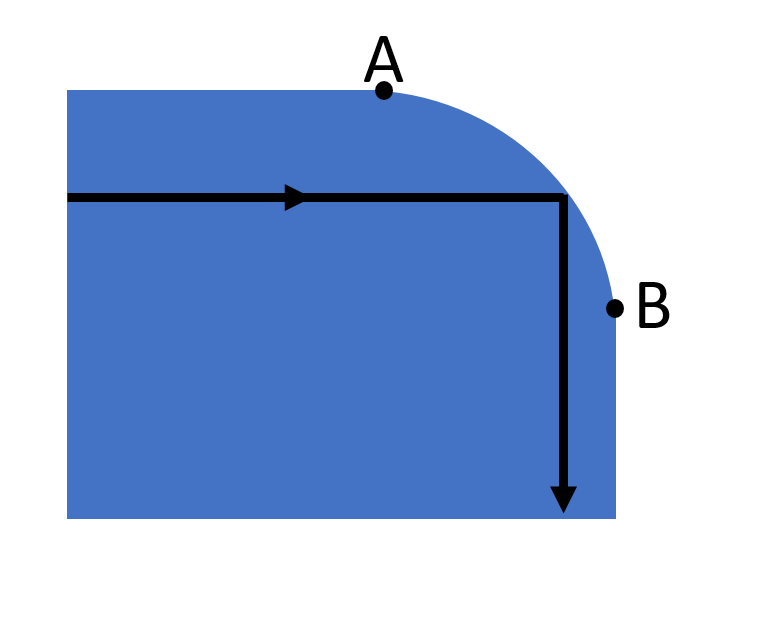
-
April 28, 2021 at 7:29 pm
Taylor Robertson
Ansys EmployeeHello Nouman,
This geometry problem of connecting two points smoothly could be accomplished an infinite number of ways all of which would require some scripting. I could imagine using ellipses (circles object r1 =a, and r2 =b) or bezier curves (waveguides objects), clothoid etc. None of those would have a constant radius of curvature. If you want to use a circle then the key insight would be that these two points would be on a common arc. The centre point, and central angle could then be calculated for a given radius of curvature. I think the other choices seem to me a bit easier to implement, but I think that if you googled "Set the parametric equation of an arc with two points" you could find a derivation.
Maybe you have a solution that you could share with us?
Best Regards,
-
April 28, 2021 at 8:28 pm
noumanzia
SubscriberThank you!
Already found the solution:
R = 300e-6;
px1 = 0;
px2 = 50*1e-6;
py1 = 50*1e-6;
py2 = 0;
# add curved mirror
x = linspace(px1,px2,500);
L = sqrt((px2-px1)^2+(py2-py1)^2);
theta = 2*asin(L/2/R);
phi = pi/4-theta/2;
yc = py2-R*sin(phi);
xc = px2-R*cos(phi);
y = yc + sqrt(R^2-(x-xc)^2);
x_positions = [0;x];
y_positions = [0;y];
addpoly;
set("name", "curved_mirror");
V=[x_positions,y_positions];
set("vertices",V);
set("x",0);
set("y",0);
-
July 11, 2022 at 6:03 pm
jackzhf
SubscriberYou are on the right track. Use the two points to define the center of the circular curve and confine the center and radius accordingly.
-
Viewing 3 reply threads
- The topic ‘Bend arc between two fixed points’ is closed to new replies.
Ansys Innovation Space


Trending discussions


Top Contributors


-
3727
-
1328
-
1163
-
1090
-
1014
Top Rated Tags


© 2025 Copyright ANSYS, Inc. All rights reserved.
Ansys does not support the usage of unauthorized Ansys software. Please visit www.ansys.com to obtain an official distribution.







