TAGGED: fluent, Fluid Volume, piece-wise-polynomials
-
-
March 19, 2024 at 8:42 am
Dato
SubscriberHello everyonr,
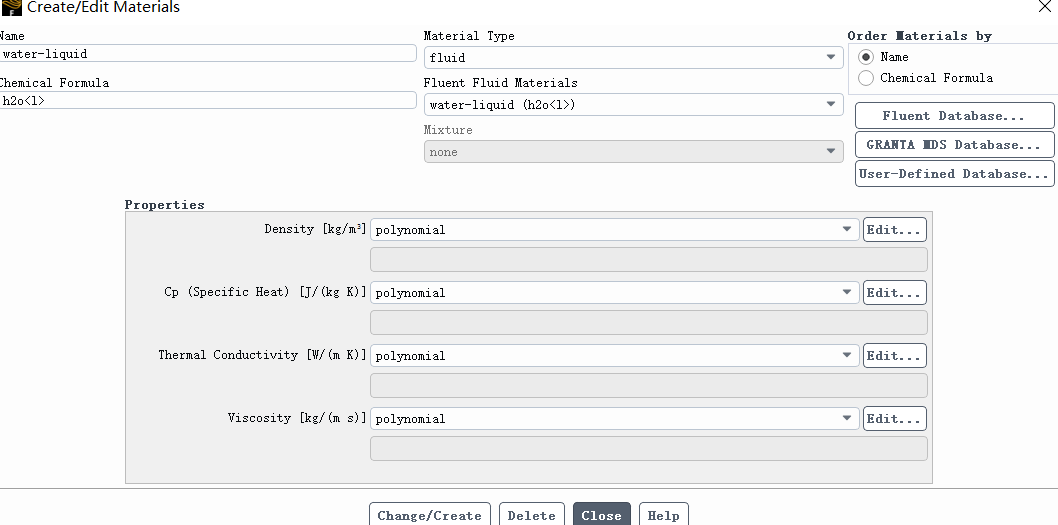
I'm simulating a steady internal cylindrical pipe flow of water with constant heat flux on the wall. I have exported water thermal properties and fit them using polynomial ranging from 280℃ to 373℃ in Origin. Four properties are all fitting using polynomial.
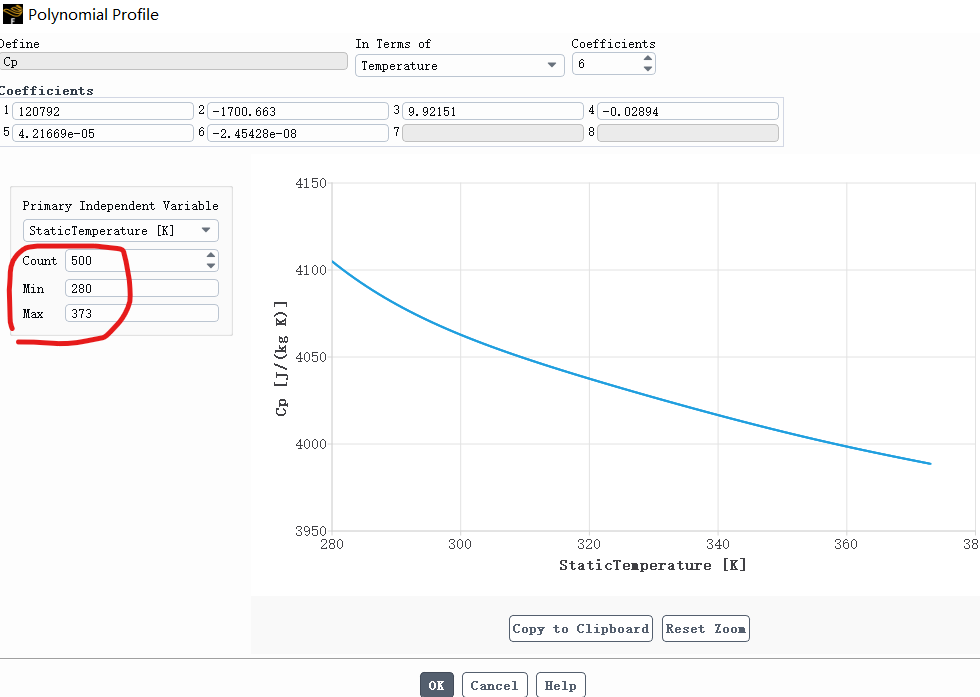
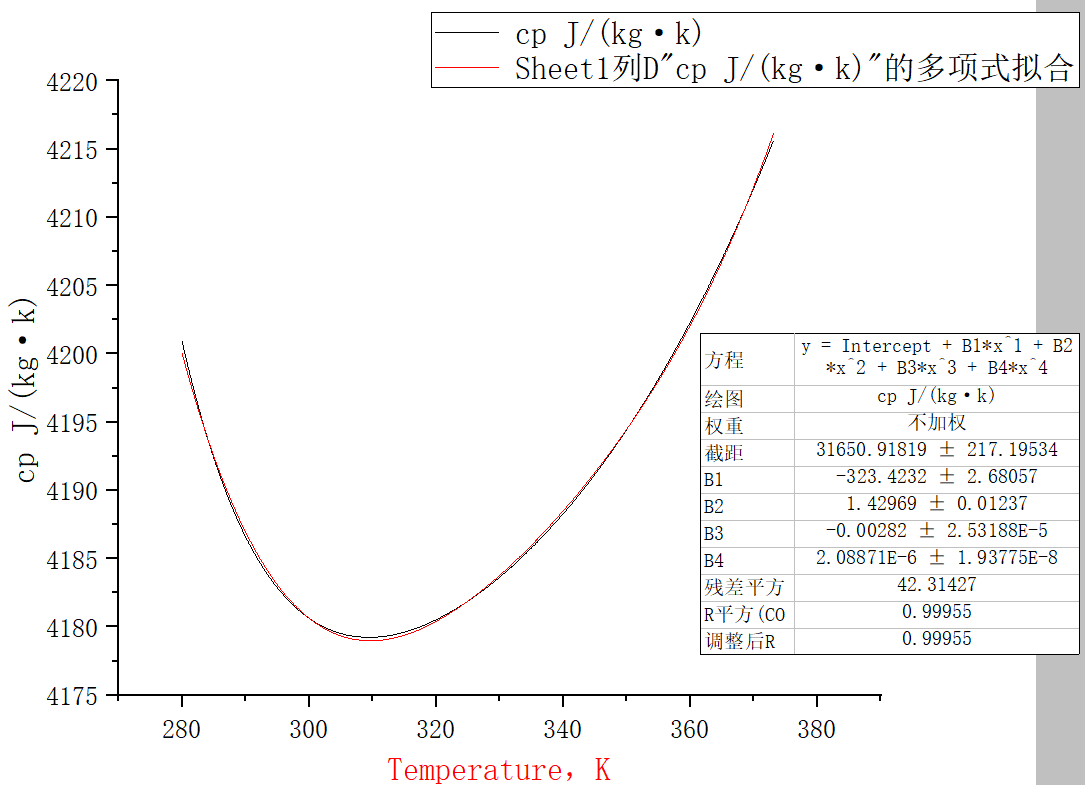
But the curve is totally different from origin one in same range as showing below. Let's take Cp for an example.
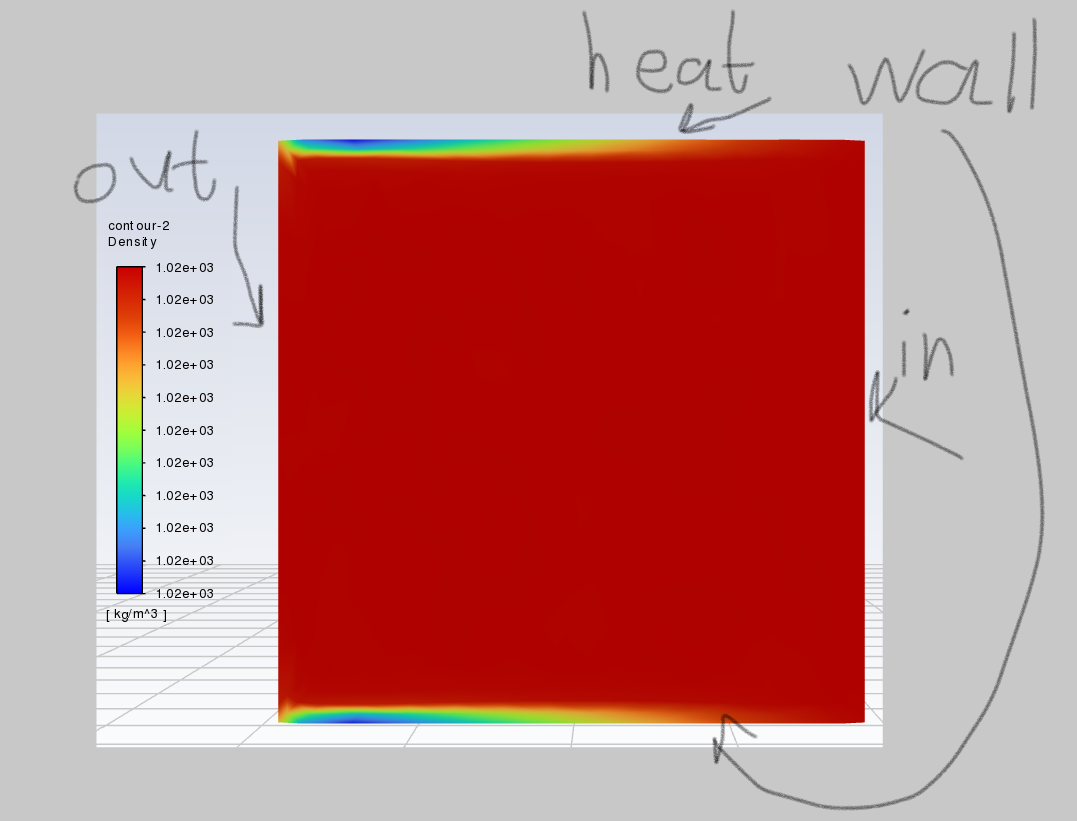
And after I run my simulation and it converged. I checked the density contour. The ranging density is unreasonably higher than that in ordinary temperature. It's weird that water is heated and its density is supposed to decrease when fluid temperature is increasing. The density contour is shown below.
Same problems as Cp. Maximum Cp is far more lower than minimum value of the fitting curve.
It almost drives me mad these days. I have try different ways to apply polynomial fitting function like expression and UDF.But it seems that the outcome is almost the same.
Anyone could help explain it and how do you guys apply polynomial properties in Fluent?
Regards.
-
March 19, 2024 at 12:15 pm
Rob
Forum ModeratorLooking at the Fluent coefficients and the ones in the graph (and noting I have no idea what the characters mean) they look very different. Please can you double check you've used the correct polynomial coefficients? I'm also very suspicious of any correlation that relies on a power 5 exponent with a multiplier of 1x10^-7 as the numerical precision is far too likely to produce rubbish when rounding errors are taken into account: would you those values in an experimental report? Piecewise linear is often a much safer option.
-
March 20, 2024 at 1:37 am
Dato
SubscriberHi Rob,
Sorry that I post different graphs of fitting curve and Fluent coefficents. I have try using 5 and 4 orders polynomial coefficents. The characters shown in the graph means the polynomial coefficents and the correation coefficient of polynomial formulation have reached to alomst 1. I'm sure that I entered same coefficents but the results are not that physically reasonable. I'm using the same polynomial as literature writting. I have considered piecewise linear but it cannot completely fit the water property curve ranging from 280K to 373K in 0.101Mpa so there is no wonder that the simulation would be as same as reality as possible like polynomial. Could you please give out any suggestions? Should I decrease the coefficients order though it will lose some precision to some degree?
Thanks
-
-
March 20, 2024 at 10:49 am
Rob
Forum ModeratorThe problem with the data you're taking from literature is it's 1.12345 x T^5 (for example), so 1.12345 x 350^5 if you do the sums how far off are you if you did the same with 1.234556 xT^5 ? Hence the use of piecewise linear tends to be safer. The error at a specific point will likely be far smaller than the rounding error multiplying a factor by 5,252,187,500,000 !
-
March 21, 2024 at 7:07 am
Dato
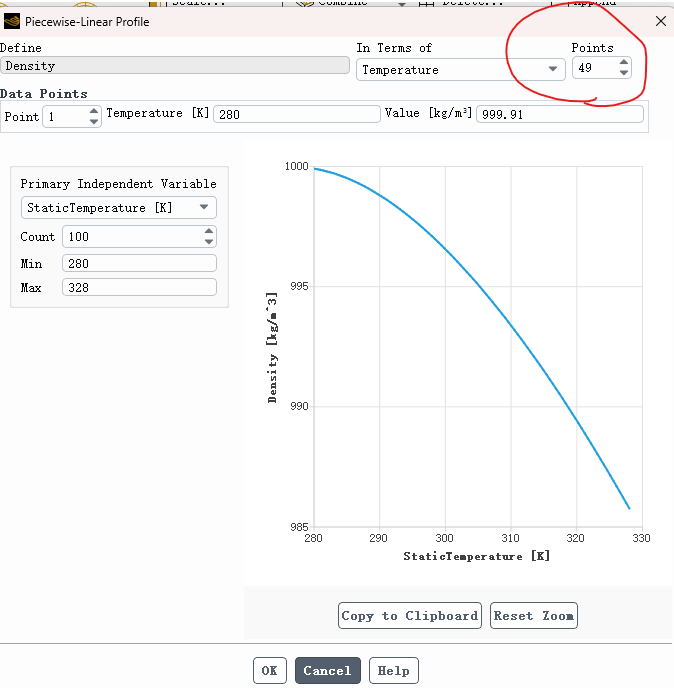
SubscriberDear professor, I'm really grateful for your advices. I hace try piecewise-linear and get a much more reasonable simulation compared to polynomial. Unfortunately, I found that we can only enter 49 points to describe the fitting curve as shown below. If the temperature of fluid in domain ranging in a larger extents, it couldn't satisfy desired accuracy compared with polynomial. Meanwhile, we need to take care when using polynomial because of rounding errors. I want to know Fluent support more points inputs to cover a larger range so that we can a higher precision using some methods like TUI?
-
-
March 21, 2024 at 11:02 am
Rob
Forum ModeratorHow complicated is the curve to need that many points? If I asked you to go into the lab and measure the temperature at a particular point in the domain, how precise would that be? Consider both the absolute position of the measurement along with the measurement precision.
-
March 23, 2024 at 1:32 am
Dato
SubscriberI see. Thanks you, professor.
-
-
- The topic ‘unresonable result when using polynomial fitting properties’ is closed to new replies.



-
5094
-
1831
-
1387
-
1248
-
1021

© 2026 Copyright ANSYS, Inc. All rights reserved.