Learning Forum

[Alex]

Hello,
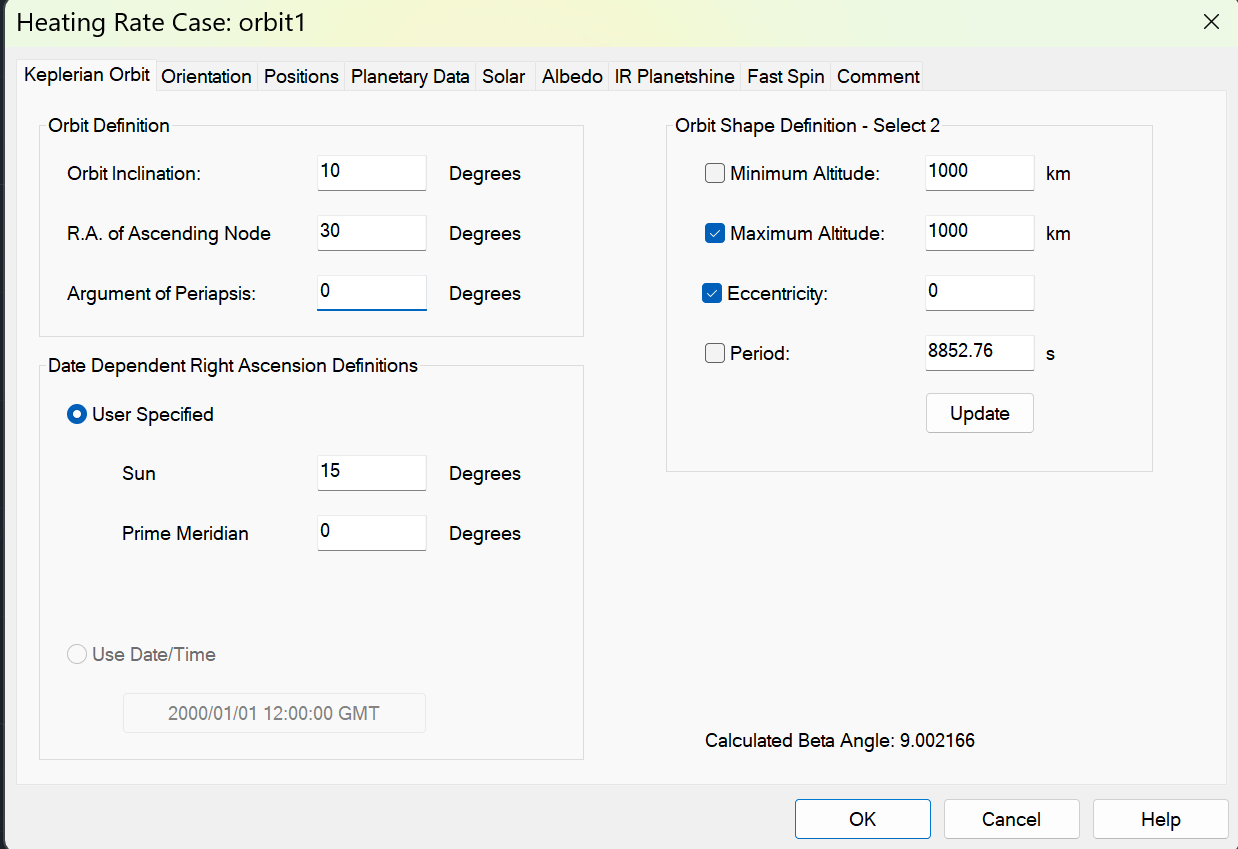
When creating an orbital heating rate case around a non-Earth planet in Thermal Desktop, what coordinate system are the Keplerian orbital elements defined with respect to? For instance, for a Mars orbiting spacecraft, are the elements defined relative to some sort of inertial frame centered about the body (Mars-Centered Inertial), the international celestial reference frame (ICRF), or something else? Details about the specific frames for the default orbiting bodies are much appreciated!

[Doug Bell]

Please see Section 6.3.2 Keplerian Orbit of the Thermal Desktop manual for a definition of the orbital elements. A Keplerian orbit uses the RA Sun to determine the position within the central body's year (orbit about the Sun).

Let me know if you found this helpful or have other questions or concerns.

Kind regards,

Doug

[Alex]

Thank you, Doug. May you also please provide the formulas that Thermal Desktop uses to calculate the solar declination and beta angle? My hand calculations for Beta angle are not matching the internally calculated values by Thermal Desktop.

[Doug Bell]

Can you provide the inputs you are using that are producing the values in question?

[Alex]

Here is a brief MATLAB script I use to calculate a Beta Angle of about 8.80982 degrees for a spacecraft in a circular Mars orbit, compared to Thermal Desktop's calculated Beta Angle value of about 9.00216 with the same inputs:

L_s = 15; % longitude of sun (right ascension of sun)

orbInc_deg = 10; % relative to planet equator

orbRAAN_deg = 30; % from planet vernal equinox direction

equatorInc_deg = 25.19; % axis of rotation tilt relative to the ecliptic plane (inclination of equator relative to ecliptic plane)

decSun_deg = asind(sind(equatorInc_deg)*sind(L_s)); % solar declination relative to planet equator

BetaAngle_deg = asind((cosd(decSun_deg)*sind(orbInc_deg)*sind(orbRAAN_deg - L_s)) + (sind(decSun_deg)*cosd(orbInc_deg)))

[Doug Bell]

We are looking into this. We will let you know what we find.

[Doug Bell]

Thermal Desktop computes the beta angle from a series of transformation matrices calculated to relate the orbital coordinate system to a celestial coordinate system. They are the matrices used for graphics display and for computing the solar vectors in the vehicle coordinate system. Embedded in the process is the same equation for beta angle you cited.

The difference is the declination formula. We use ecliptic longitude (measured in the ecliptic plane) instead of right ascension (measured in the equitorial plane).

[Alex]

Hi Doug,

1. It sounds like you are saying the equatorial right ascension (15 degrees in my TD screenshot) is converted by Thermal Desktop to an ecliptic longitude to calculate the solar declination parameter. Is that correct? May you please provide the formula or matrices for this conversion?
2. In the BetaAngle_deg function from my previous post, I have a parameter sin(orbRAAN_deg - L_s). Should the L_s variable that appears here be the equatorial right ascension of the sun (15 deg) or should it also be converted to the ecliptic longitude form?

Thank you for all your help so far! I am trying to validate my own model with Thermal Desktop, so accuracy is important.

[Doug Bell]

I was mistaken in my earlier post. The difference between our calculations is the approximation of the declination. We are using the equation (using your variable names):

decSun = orbInc*sin(L_s)

This yields the Beta angle shown on the orbit form and used in the calculations. If you need to match a precise Beta angle, you can use a basic (circular) orbit where you specify the Beta angle or you can adjust the RA Sun to get the desired Beta angle. Please note that RA Sun and Beta angles are assumed to be constant over the solution so there is a limit to how precise you can get.

[Alex]

 

Thank you. My calculations and the ones done by Thermal Desktop now match! Copying my sample script below in case it is useful to others:

sunRA_deg = 15; % right ascension of sun in equatorial plane

orbInc_deg = 10; % relative to planet equator

orbRAAN_deg = 30; % from planet vernal equinox direction

equatorInc_deg = 25.19; % axis of rotation tilt relative to the ecliptic plane (inclination of equator relative to ecliptic plane)

decSun_deg = equatorInc_deg*sind(sunRA_deg); % Thermal Desktop approximation of solar declination relative to planet equator

BetaAngle_deg = asind((cosd(decSun_deg)*sind(orbInc_deg)*sind(orbRAAN_deg - sunRA_deg)) + (sind(decSun_deg)*cosd(orbInc_deg)));