Learning Forum

[Brian Lolley]

Hello,

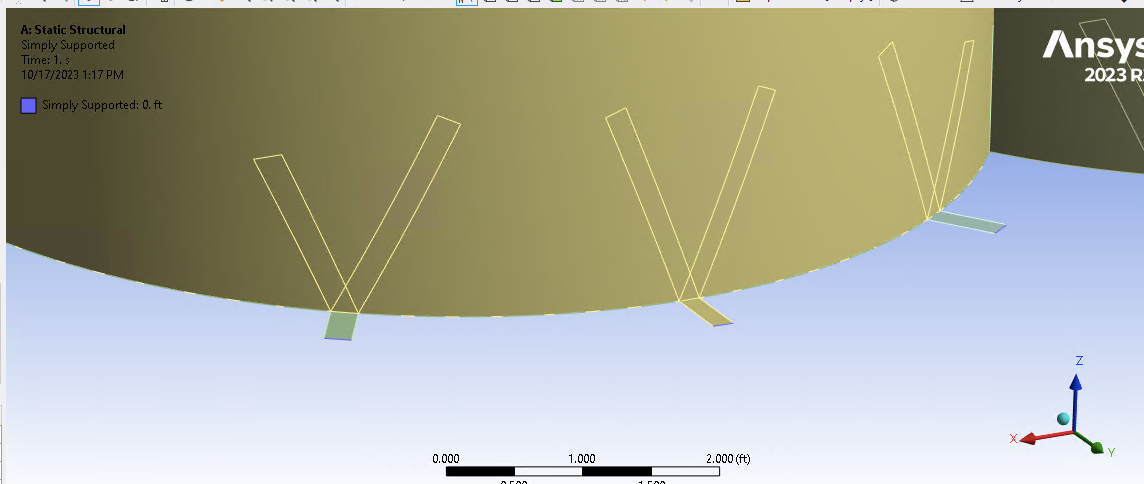
I have modeled an inflatable structure with a membrane that is hyperelastic. I used the Mooney-Rivlin 5 Parameter equation to fit a curve to my uniaxial data to get a nonlinear stress-strain curve. I have modeled two structures. One structure has straps modeled and the other does not. The model without straps works when doing nonlinear analysis, but the model with straps (the straps themselves have linear material properties) does not work with nonlinear analysis. The one with straps does work when using linear materials, so the geometry should not be the problem. As seen below, the structure is simply supported on edge of the straps that sticks out away from the structure. To sum up: I know my nonlinear material properties work, I know my geometry works, but when I try the two together I get the error seen below. Any ideas how I can fix this problem?

Thanks,

Brian

[Akshay Maniyar]

Hi Brian,

It looks like your model is not converging. Can you request Newton-Raphson residual plots and check which is the problematic location? As per your description, the issue might be in contact between the strip and the remaining geometry.

Thanks,

Akshay Maniyar

 

[Brian Lolley]

Akshay,

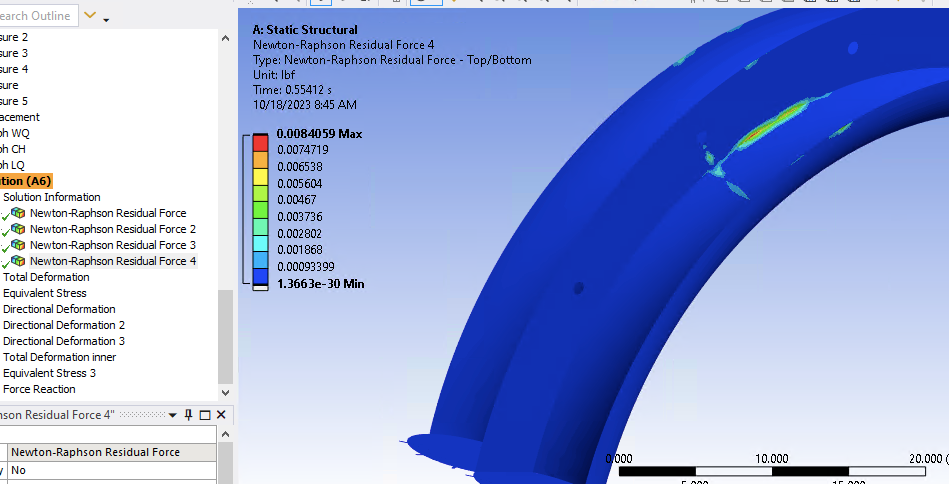
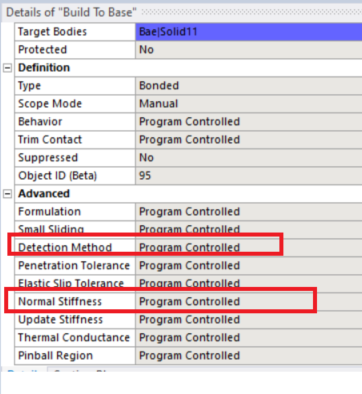
Thank you for your response. I made the Newton-Raphson residual plots and surprisingly it showed that the problem is not at the straps. The problem is at one of the inner membrane and outer membrane connection points. I created manual connection points and double checked that they are properly connected at the troubled point. I have read that changing the detection method for contact elements from program controlled to Nodal-Normal to target. Also, reducing contact stiffness by changing the normal stiffness from program controlled to 0.2. I do not see where these settings are to change them though. Do you know where they are located or of any other solutions?

Thanks,

Brian 

[Akshay Maniyar]

Hi Brian,

The settings you mentioned will be under the details of contacts. Please check the contact for which the problematic surfaces are part, make necessary changes, and try running it again.

Thanks,

Akshay Maniyar