Learning Forum

[Jo Cruz]

Hello Ansys Community,

 

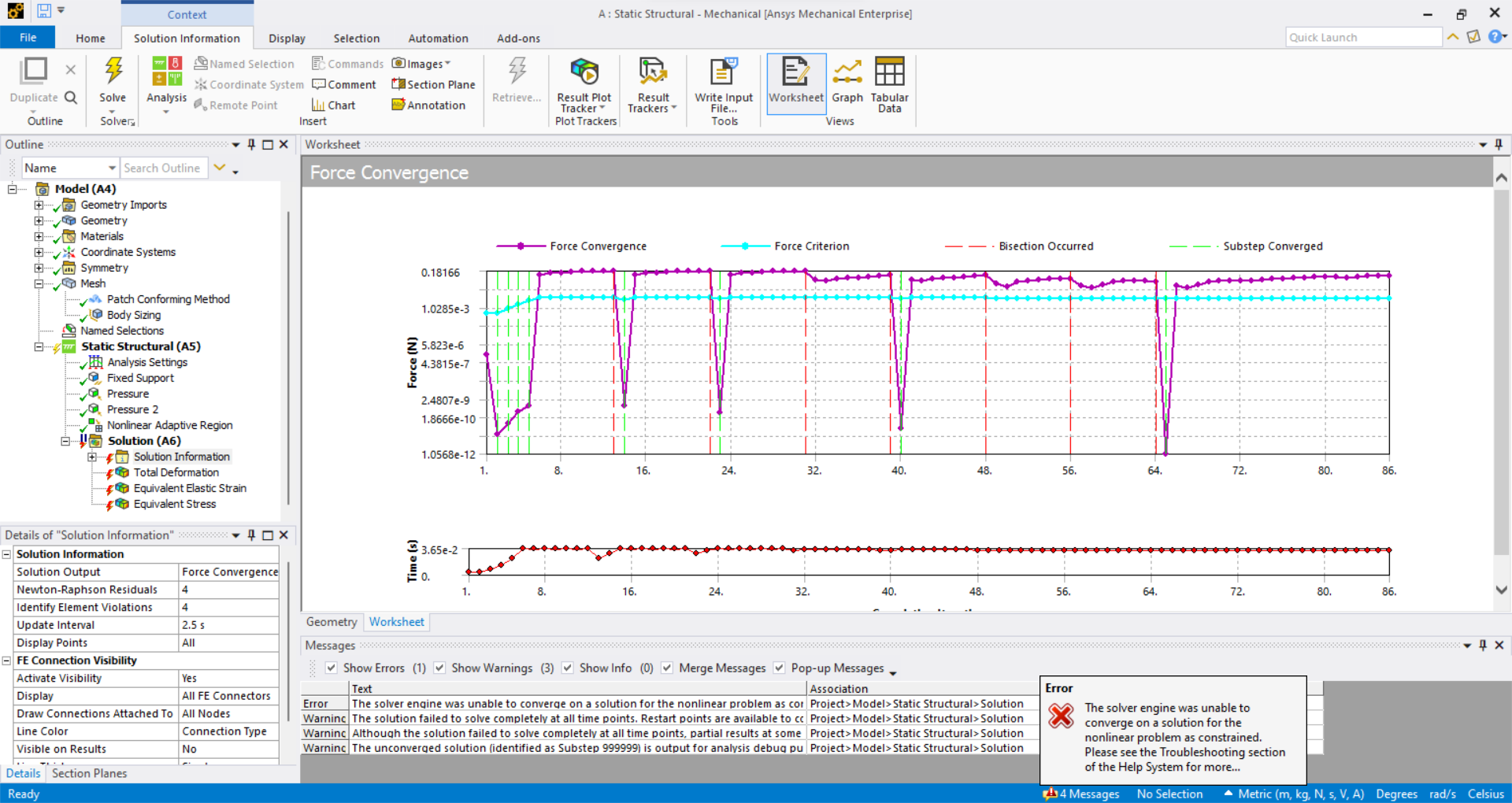
I am trying to simulate an unconsolidated undrained triaxial compression test through static structural analysis, however, the software keeps on telling me that it doesn’t converge to a solution. My goal is to create a similar stress-strain curve in the software with the experimental results that I have. What I did is that I created a Soft Clay material with a Mohr-Coulomb model and after that, I created the cylinder model under triaxial compression but I am not sure if I used enough boundary conditions. I would also like to add that this is nonlinear. 

 

The following screenshot is what happens and I can't seem to move forward from this.

 

 

I am not sure what data I should show but if anyone can help I am willing to give what is needed for your understanding. 

[peteroznewman]

Hello Jo Cruz,

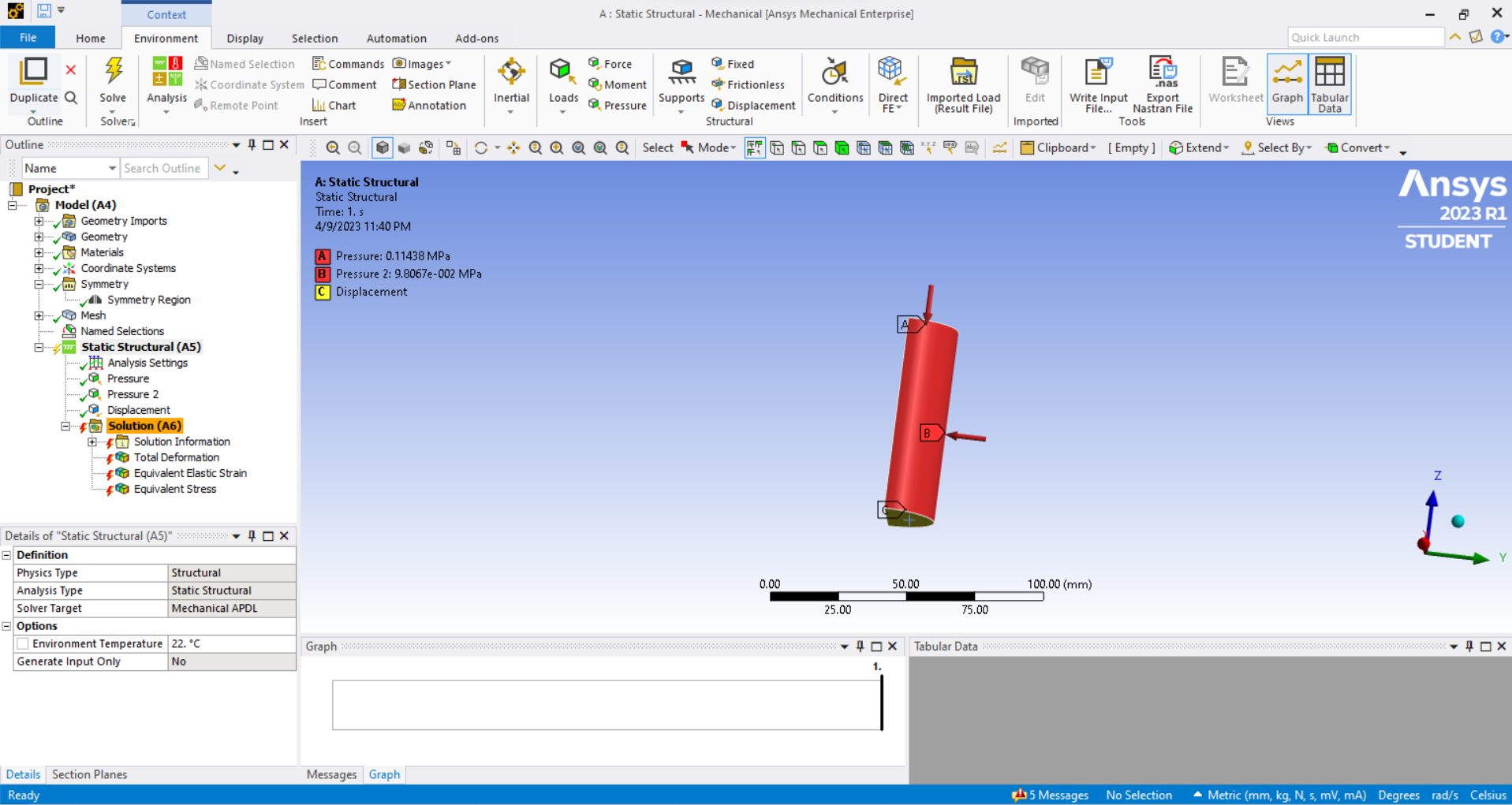
Fixed Support may be hurting the convergence. I assume that is at the bottom of your model. If you have two vertical planes of symmetry and two faces with applied pressure that push the model onto those two symmetry planes, the bottom only needs a simple Displacement boundary condition to set the vertical DOF to 0.0 and leave the lateral DOF free. Then you can delete the Fixed Support.

Regards,
Peter

[Jo Cruz]

Hello Peter,

Thank you so much for that suggestion. I have followed your instructions, however, I am receiving an error that not enough constraints are applied. The model can be seen below as well as the errors from the solution information. 

 

What seems to be the problem here? 

 

Regards,

Jo

 

[peteroznewman]

Hello Jo,

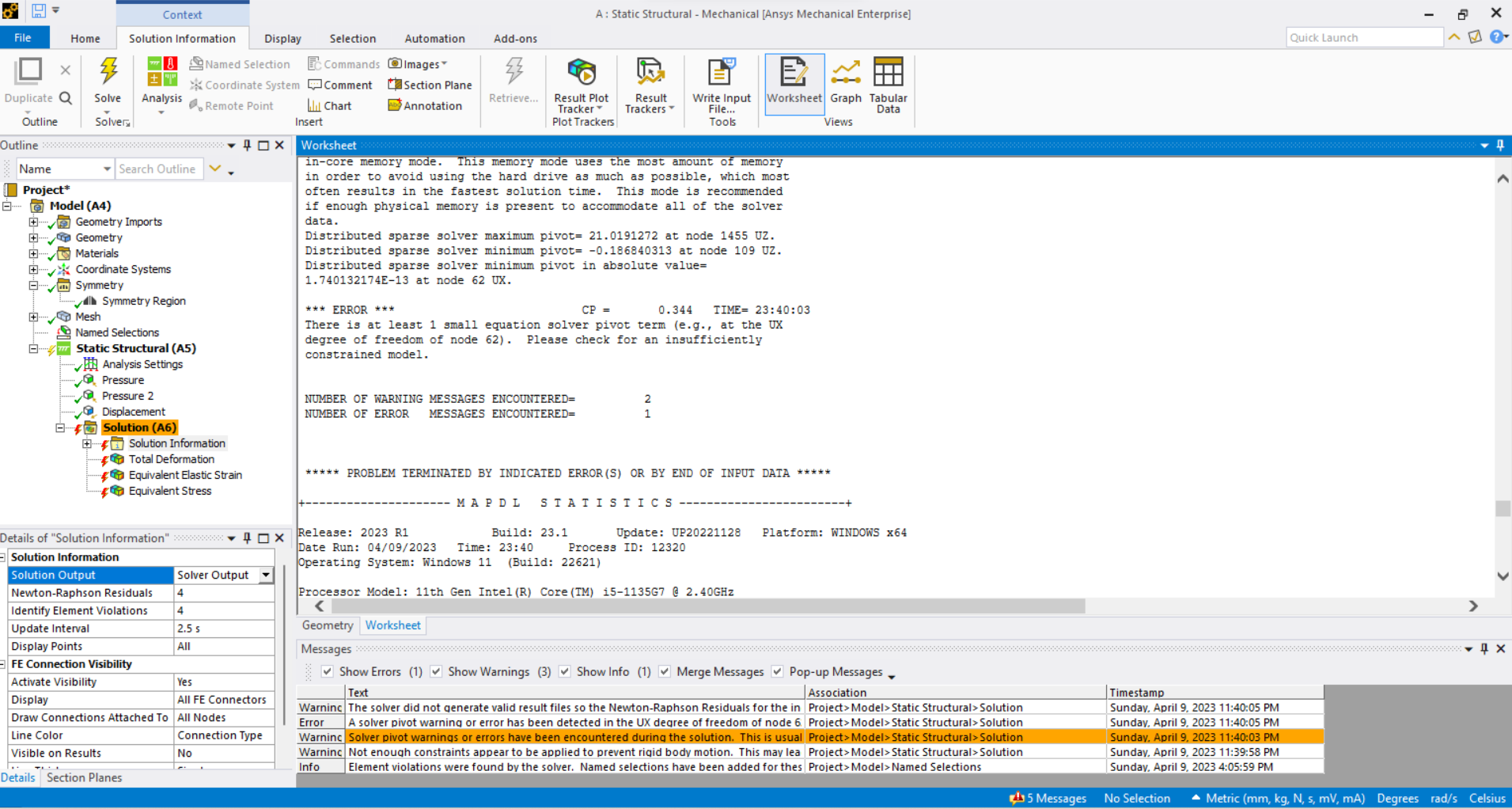
Since you have only one symmetry plane, there is no constraint to prevent motion along the X axis.

Split the body with a plane at 90 degrees to the first symmetry plane through the center of the circle. That symmetry boundary condition will prevent motion along the X axis.

Regards,
Peter

 

[Jo Cruz]

Hello Peter,

 

Thank you again. Is this what you mean about splitting the body?

 

If yes, I reapplied the boundary conditions which is shown on the image below.

 

I apologize for asking step by step, I just want to make sure that I'm doing it correctly. Thank you again!

 

Regards,

Jo

[peteroznewman]

Hello Jo,

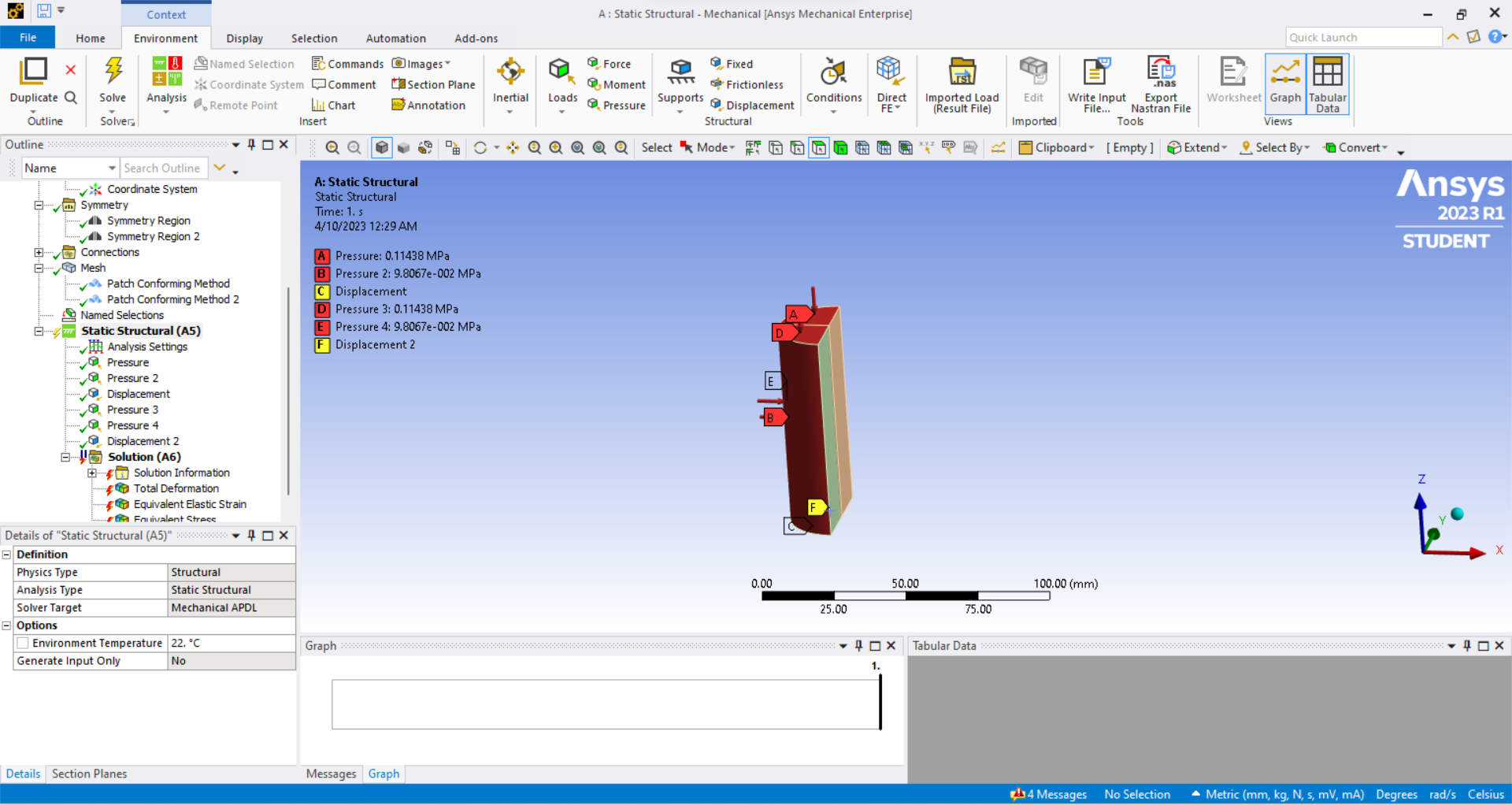
In Mechanical, suppress the brown body (or in SpaceClaim, suppress for Physics).

In the 1/4 circle that remains, the face that has a normal on the X axis has a Displacement of X = 0 and Y, Z are Free.  The face that has a normal on the Y axis has a Displacement of Y = 0 and X and Z are Free. This is what the Symmetry regions do for you. You don't need both Displacement and Symmetry, but if you use Symmetry, you must have two separate ones and set the Normal axis correctly in each one. There are often three ways to do the same thing so Frictionless Support on any of those three flat faces is equivalent to the Displacement or Symmetry methods to support those faces.

Regards,
Peter

[Jo Cruz]

Hello Peter,

 

I understand it clearly now. However, when I placed the pressure on the 2 faces, it still doesn't converge. What I did is I replaced the pressure with a displacement at the top face and indicated the expected displacement from the experimental results that I have. Fortunately, it gave me results but I am not sure if it is reliable. I would like to ask if what I have done is okay or should I stick with applying the pressure. 

 

Thanks again.

 

Regards,

Jo

[peteroznewman]

Displacement is a good substitution and you can calculate the pressure from the reaction force and the area.

[Jo Cruz]

Hello Peter,

 

Thank you! I still have a few questions about the validation and verification of my model. Is it possible to ask for your email to discuss this with you in detail?

 

Regards,

Jo

[peteroznewman]

Hello Jo,

You can ask detailed questions on the forum, which is better than email in my opinion. I sometimes feel it is better to have a live discussion and for that I need your email to set up a meeting. Is that what you want?

Regards,
Peter

[Jo Cruz]

Hi Peter,

 

Yes, I agree that it is better to have a live discussion. When are you available?

 

Regards,

Jo

[peteroznewman]

Hi Jo,

I am in the Eastern Time Zone (New York). What city are you in? I can schedule a meeting Friday, Saturday and Sunday 9 AM - 6 PM except for lunchtime (noon-1 PM). Reply with your preferred day and time and an email address. Once I get your email address, you can edit your reply to delete your email address from this public forum.

Regards,
Peter

[Jo Cruz]

Thank you.