Learning Forum

[murali]

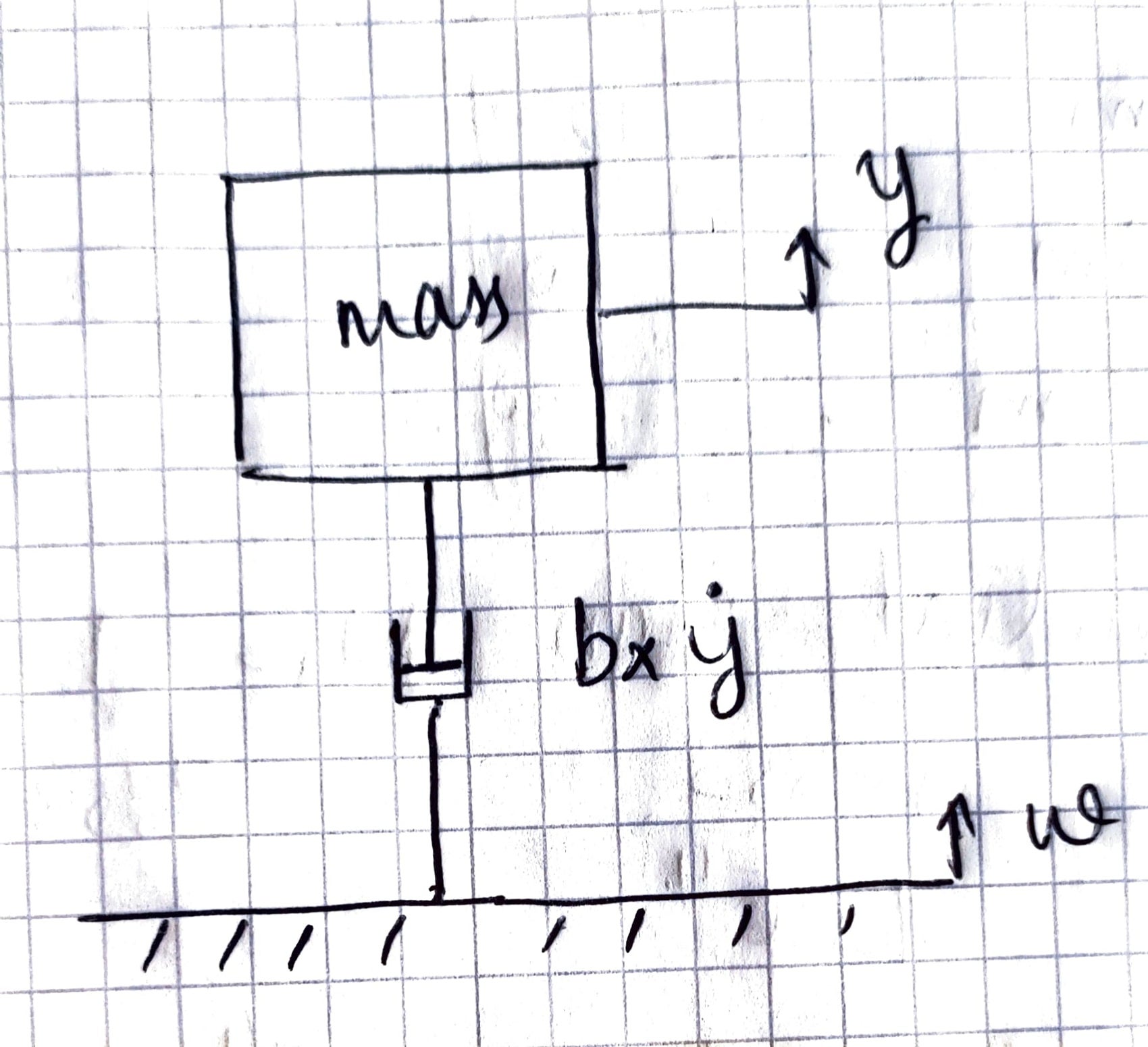
I need to model a damper producing a damping force proportional to the absolute velocity of the mass(y°) , attached to a frame which is also moving (w°). I suppose spring elements can be used as dampers, but as I understand they use the relative velocity, which is not what I require. Kindly help, if there is any way to do that in workbench.  

[peteroznewman]

Put the spring element between the mass and Ground. That will apply a damping force proportional to the absolute velocity of the mass. If the mass is moving in only one direction, you need only one spring aligned to that direction.  If you have a mass moving in other directions, you need more spring elements to provide damping in those other directions.

[murali]

My doubt is, since both frame and mass are having realtive motion, won't the spring be considering the relative velocity (b x (y°-w°)) to calculate the damping force, rather than the absolute velocity of the mass alone?

[peteroznewman]

A spring/damper between the mass and ground measures the relative velocity between the mass and ground. Since the ground is stationary, that relative velocity is exactly equal to the absolute velocity of the mass.

Another spring/damper between the mass and the frame measures the relative velocity between the mass and the frame as you have shown in your sketch. It is up to you if you want to have that spring/damper in your model or not. If not, then the motion of the mass is unaffected by the motion of the frame.

[murali]

Hello Peter,

The point is clear. I will try that. Thanks a lot.

[Chandra Sekaran]

The theroy manual section 14.3 (link below) describes the various kinds of damping supported in ANSYS. The combin14 damping is indeed based on the relative velocity. But you can use Matrix27 to input damping directly or use alpha/beta damping which are mass/stiffness proportional damping coefficients. These all will create forces proportional to absolute velocity.

https://ansyshelp.ansys.com/account/secured?returnurl=/Views/Secured/corp/v241/en/ans_thry/thy_tool3.html

[murali]

 

Hello,

Unfortunately, the link pasted in ansys help tab shows no results. Same is the case with cople of other links from other discussions.

 

[murali]

Hello Chandra,

How do we use the Matrix27 in workbench for this particular task? I am not familiar with APDL and coding. Kindly help.

 

[murali]

Hello,

How do we use the Matrix27 in workbench for this particular task? I am not familiar with APDL and coding. Kindly help.

 

[peteroznewman]

Do not paste the URL provided into the Search field of Ansys Help, paste it into the Address field of the browser at the top of the window.

[Erik Kostson]

Hi

 

See here how to access the help links we provide (as in the above post):

 

/forum/forums/topic/how-to-access-the-ansys-online-help/#:~:text=Here's%20how%20you%20can%20access,on%20the%20Ansys%20Learning%20Forum.

All the best

 

Erik

[Chandra Sekaran]

For using matrix27, you will need to use command snippets. It does require familiarity with APDL.  Using global damping like alpha and beta is more straightforward as it is supported in Mechanical directly. Please see section 1.2 of the structural analysis guide (MAPDL help). Here is an excerpt on alpha and beta.

1.2.1. Alpha and Beta Damping (Rayleigh Damping)

Alpha damping and Beta damping are used to define Rayleigh damping constants α and β. The damping matrix [C] is calculated by using these constants to multiply the mass matrix [M] and stiffness matrix [K]:

[C] = α[M] + β[K]

The ALPHAD and BETAD commands are used to specify α and β, respectively, as decimal numbers. The values of α and β are not generally known directly, but are calculated from modal damping ratios, ξ_i. ξ_i is the ratio of actual damping to critical damping for a particular mode of vibration, i. If ω_i is the natural circular frequency of mode i, α and β satisfy the relation

ξ_i = α/2ω_i + βω_i/2

In many practical structural problems, alpha damping (or mass damping) may be ignored (α = 0). In such cases, you can evaluate β from known values of  ξ_i and ω_i, as

β = 2 ξ_i/ω_i

Only one value of β can be input in a load step, so choose the most dominant frequency active in that load step to calculate β.

To specify both α and β for a given damping ratio ξ, it is commonly assumed that the sum of the α and β terms is nearly constant over a range of frequencies (see Figure 1.1: Rayleigh Damping). Therefore, given ξ and a frequency range ω₁ to ω₂, two simultaneous equations can be solved for α and β:

Figure 1.1: Rayleigh Damping

Alpha damping can lead to undesirable results if an artificially large mass has been introduced into the model. One common example is when an artificially large mass is added to the base of a structure to facilitate acceleration spectrum input. (You can use the large mass to convert an acceleration spectrum to a force spectrum.) The alpha damping coefficient, which is multiplied by the mass matrix, will produce artificially large damping forces in such a system, leading to inaccuracies in the spectrum input, as well as in the system response.

Beta damping and material damping can lead to undesirable results in a nonlinear analysis. These damping coefficients are multiplied by the stiffness matrix, which is constantly changing in a nonlinear analysis. Beta damping is not applied to the stiffness matrices generated by contact elements. The resulting change in damping can sometimes be opposite to the actual change in damping that can occur in physical structures. For example, whereas physical systems that experience softening due to plastic response will usually experience a corresponding increase in damping, a Mechanical APDL model that has beta damping experiences a decrease in damping as plastic softening response develops.

Damping for contact elements and MPC184 constraint and joint elements is restricted. See element descriptions for details.

 

[murali]

Hello Chandra,

Thanks for the details. My question was as to how to apply this to a spring element. Although workbench permits to give alpha and beta damping in material level and global level, how can we practically model a spring element as a damper so that it does not take the relative velocity but takes the the absolute velocity of one of the bodies it is attached to?

As Peter mentioned, attaching it to the ground is sensible. But when the connection is between two bodies, how to achieve it?