Learning Forum

[matthias.zeller]

Hello,

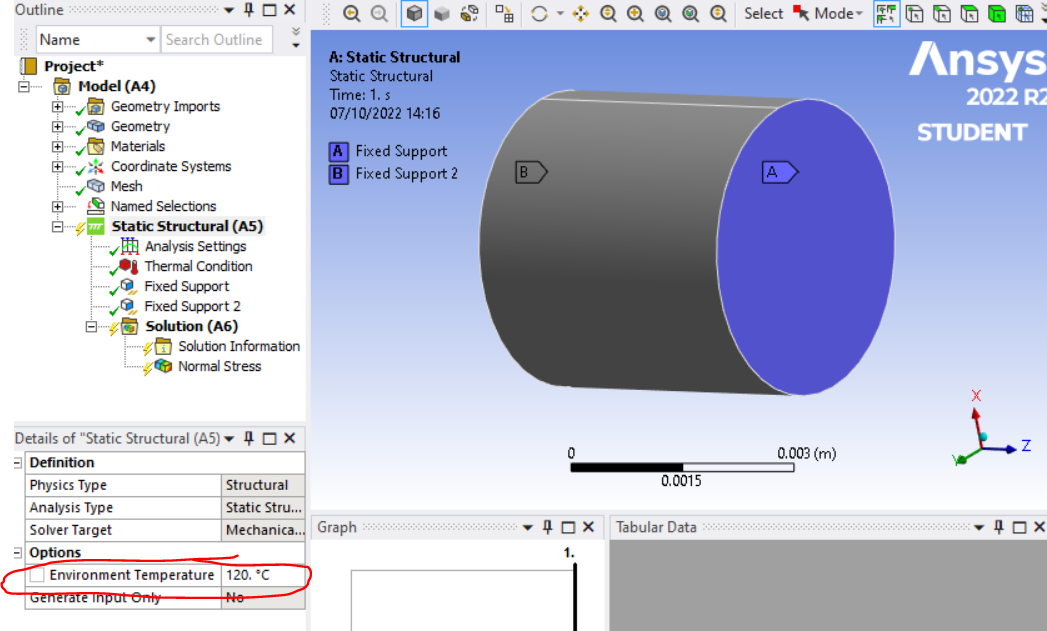
I am doing a static structural analysis on a plate which has a fixed constraint on both sides in one direction.
The material has a temperature dependent Youngs Modulus (linear), but a constant coefficient of linear expansion.

The environment temperature is 120C and the part temperature is 20C.

 

The calculated stress is exactly the same like using a constant Youngs Modulus. Why?

 

At temperatures with a lower youngs modulus there should be a smaller force/stress caused by the fixed constraint?!

It seems like Ansys calculates the thermal strain and calculates the stress based on the youngs modulus at part temperature. Is that correct?

[peteroznewman]

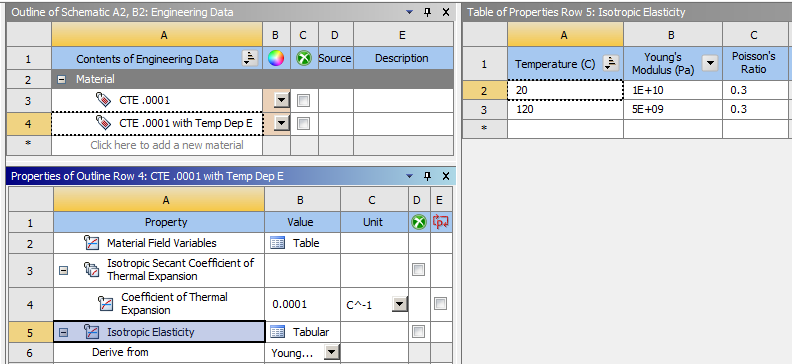
The stress for a uniform cross-section with fixed ends does change with temperature dependent properties. Below are two materials. One has a constant E of 1E+10 Pa. The Temp Dep E has the following properties:

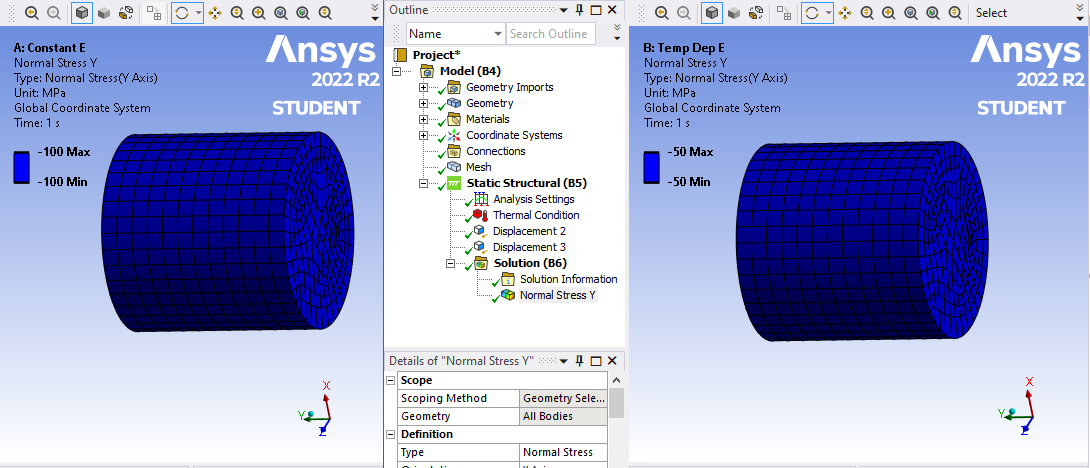
The stress is clearly lower in the Temp Dep E material.

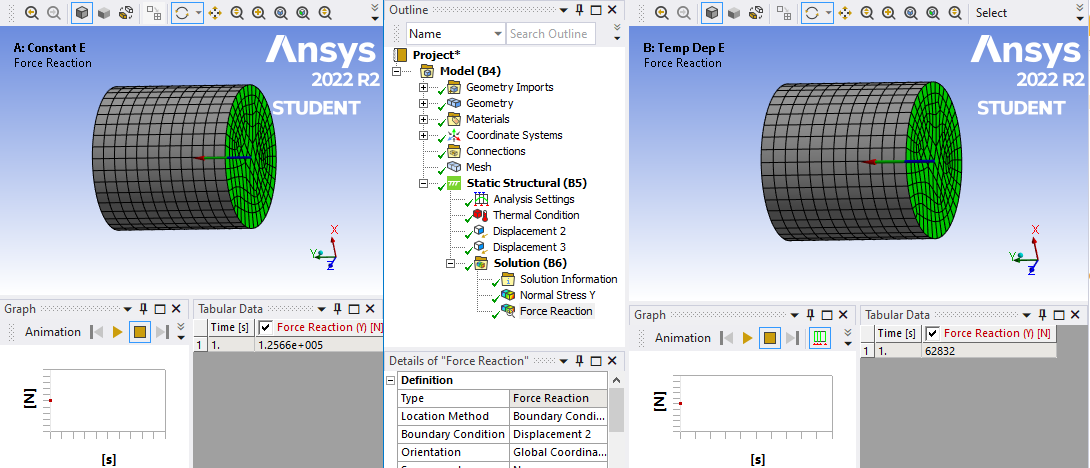
The reaction force is clearly lower in the Temp Dep E material.

[matthias.zeller]

 

Hi Peter, 

thanks for your answer!

I dont have the same result.

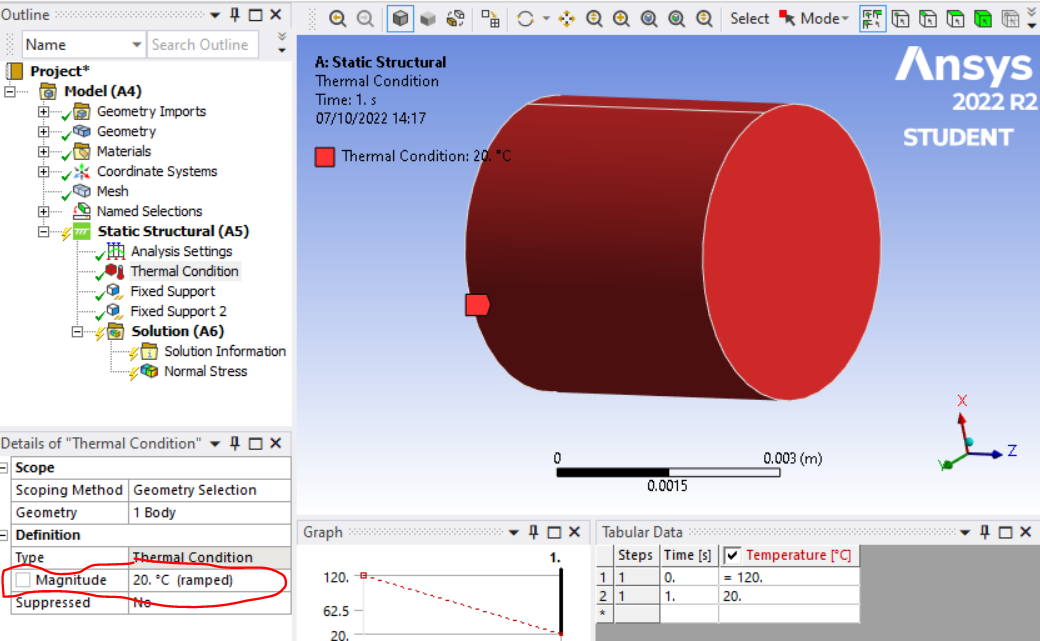
I only have the same result when changing the youngs modulus at part temperature/thermal condition (20 °C).

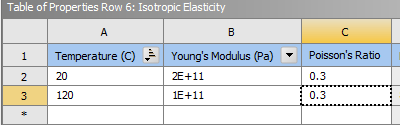
I modified structural steel by adding a lower modulus for 120 °C:

Temperature dependent:

My project looks like this:

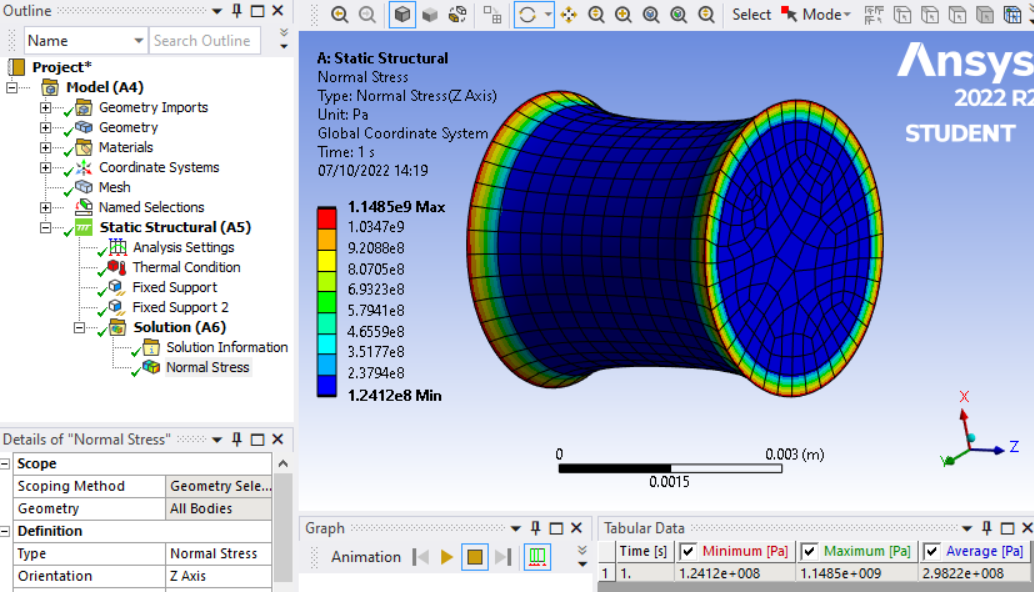
For the material with the constant youngs modulus and the temperature dependent youngs modulus it is the same result:

As said before: When I change the youngs modulus at 20 °C, there is a change. The youngs modulus at 120 °C does not influence the results.
Am I doing a mistake or what is the reason?

 

[peteroznewman]

What is the temperature when the ends are Fixed? In my model, the ends are Fixed at 20 C.  Then I apply a Thermal Condition of 120 C and stress builds up as the part expands. The Enironment Temperature is the temperature when the part is stress free. The Thermal Condition changes the temperature from the Environment Temperature to another temperature.

In your case, the ends are fixed at 120 C and you are cooling the item down and it contracts.

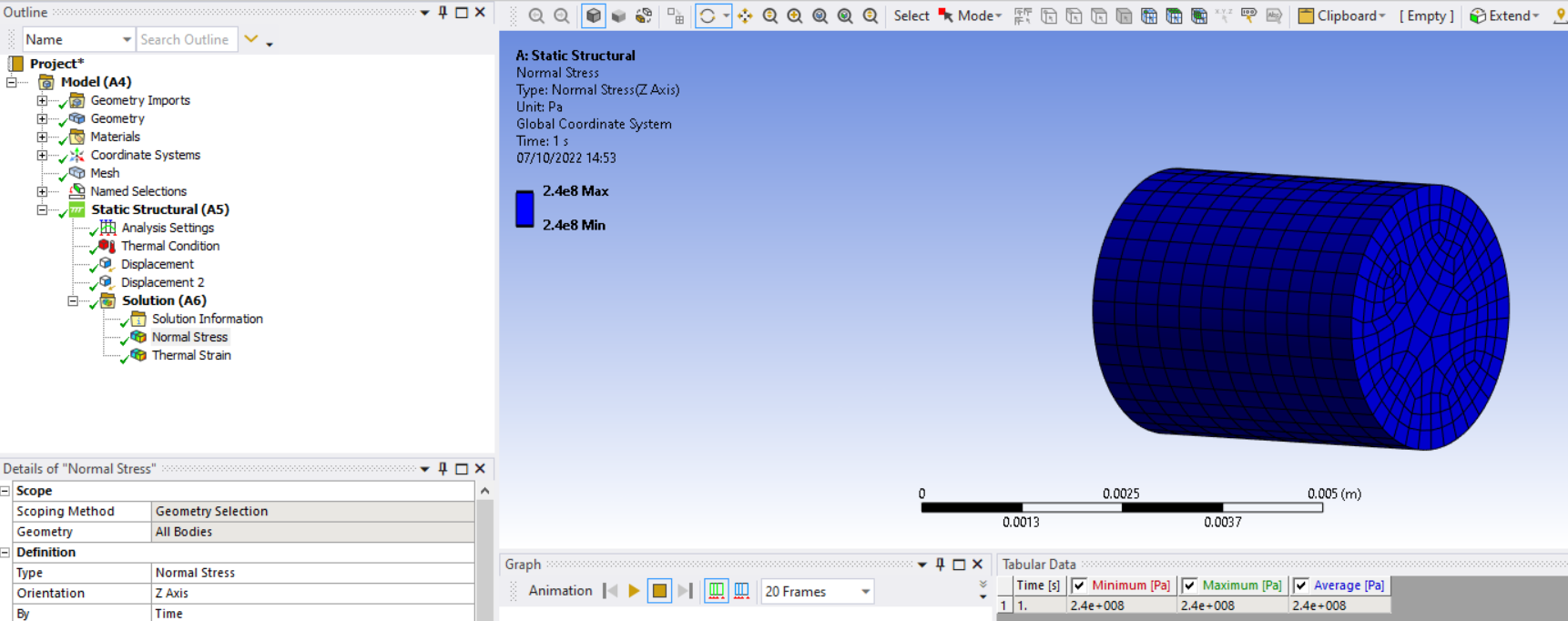
It is simpler to see a purely axial stress in the part if you use displacements to fix the ends but leave the radial direction free.  Create a Cylindrical Coordinate System on the flat circular end face. Delete the Fixed Supports. On one end face apply a Displacement, use the Cylindrical Coordinate System and Set Y and Z to 0 but leave X Free. On the opposite end face, apply a Displacement, but set only Z to 0.  Plot the Normal Stress in the Z axis and you will see a uniform axial stress.

[matthias.zeller]

 

Hi Peter,

I did the same now.
Here is the result with constant youngs modulus:

 

Here is the result with decreased (half) modulus at 120 °C:

Now I change the youngs modulus at 20 °C (half):

 

Why is there no change between the constant youngs modulus and half the youngs modulus at 120°C?

 

[peteroznewman]

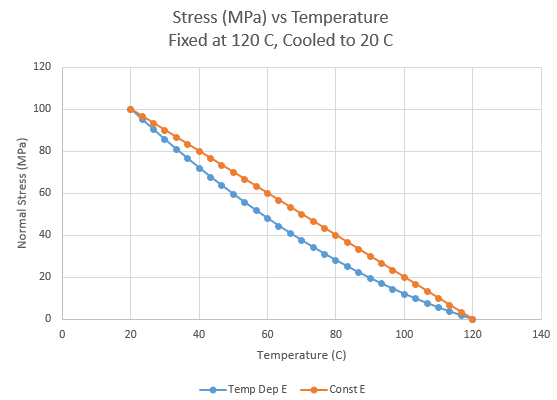
Now I understand your question. The materials have the same Young's Modulus at 20 C so they have the same stress at 20 C.  The materials have a different Young's Modulus at 120 C, but they were assembled at that temperature, so have zero stress. Only the Temperature dependent material deviates from the straight line on the way to the stress at 20 C.