-
-
February 22, 2023 at 4:41 am
Sankar Krishnan
SubscriberDear Peteroznewman
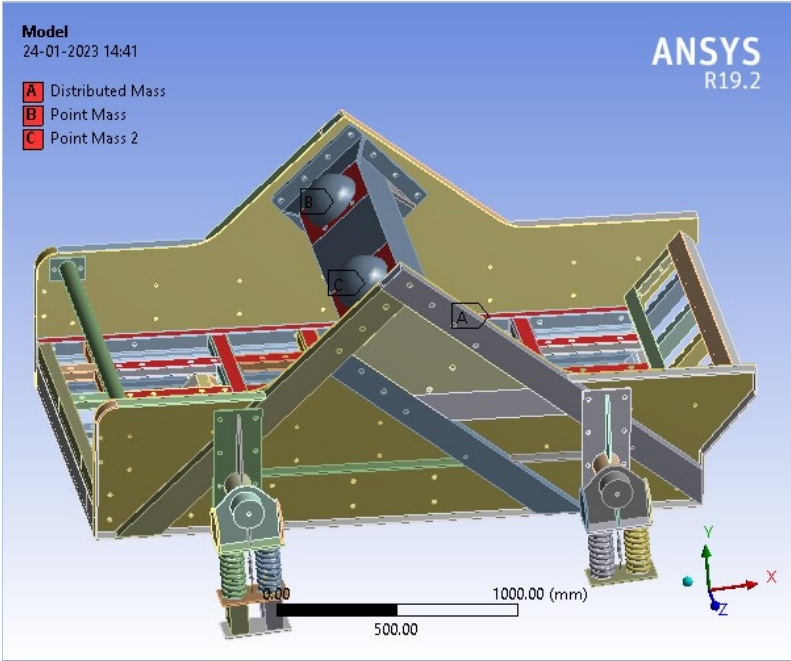
Kindly tell me the steps to be followed to find out the natural frequency of the vibrating structure as shown in the image.
Two Vibrating Motor of 16Hz is Vibrating at B & C as Shown In the image.
The structure is Mounted on the Springs, Kindly tell me the steps to follow in the modal Analysis.
@peteroznewman #peteroznewman
-
February 22, 2023 at 7:57 am
ErKo
Ansys EmployeeHi
We have some free courses on modal analysis in Mechanical
/courses/index.php/courses/modal-analysis-in-ansys-mechanical/
Hope this helps
Erik
-
February 22, 2023 at 8:17 am
Claudio Pedrazzi
Subscriberif you are looking for the natural frequencies, the "vibrating motor" at 16 Hz is not important. Just use a modal analysis system from Workbench, constrain the surfaces or points that are physically constrained and let the analysis run. If the analysis will give modes with frequencies of zero, or numerically zero, that will mean you have "free" parts in your assembly, that need to be correctly connected.
-
February 22, 2023 at 11:34 am
Sankar Krishnan
Subscriber@Claudio Pedrazzi #Claudio Pedrazzi Thank you for your valuable reply sir, if I get different modes with respective different frequencies, does the frequency that meets the vibrating motor frequency (16 Hz) at the mode of structural collapse or something mean I have to increase the stiffness of the structure, or should change the structure design. Am I correct sir?
-
-
February 22, 2023 at 12:03 pm
Claudio Pedrazzi
SubscriberIf some natural frequency of the structure (correctly constrained and with the correct masses distribution everywhere) is near the rotating frequency of the motor (or any other excitation source), of course you will get a resonance, this could cause high stresses and high vibrations. Normally this means to try make the structure stiffer or more flexible, looking for it to have no natural frequency within +- 20% of the excitation frequency. When this is practically impossible, one could try to increase damping. Hope this helps.
-
February 23, 2023 at 5:12 am
Sankar Krishnan
Subscriber@Claudio Pedrazzi I can understand the general concept, sir.
In my case, vibrating motors have their own self-weight and distribution mass over at point A. Are these two factors will affect the mode shapes and natural frequency?
Another doubt is, I am using two exciters, so the excitation frequency is double the value ( 2x 16 - 32 Hz) or Not?
whether I have to apply the moment of the exciters or not?
Totally what are the inputs I should apply to get correct natural frequency modes.
-
-
February 23, 2023 at 5:47 am
Claudio Pedrazzi
Subscriber>>In my case, vibrating motors have their own self-weight and distribution mass over at point A. Are these two factors will affect the mode shapes and natural frequency?
Of course they do. Natural frequency is influenced by mass distribution and stiffness distribution. On the contrary, the fact that they are "vibrating", this has no influence on the natural frequency. Think of the natural frequency, as the word says, of a "property" of a certain structure, constrained in a certain way. Natural frequencies and modes are like a fingerprint of a structure. So be sure to put every significant mass in the model, in the appropriate position, either with point masses or with elements having the right density.
>>Another doubt is, I am using two exciters, so the excitation frequency is double the value ( 2x 16 - 32 Hz) or Not?
It seems to me that you still mix the two concepts of free and forced vibration. For a natural frequencies (eigenfrequency) analysis, there is no excitation at all. Your structure, including the masses of the motors, will have the same natural frequencies if the motors vibrate or not. The motors will have to be represented as concentrated or distributed masses, that is all.
When you will have obtained a plausible set of natural frequencies and modes, you can make a step forward and ask yourself: ok, let's see, now I know that (e.g.) I have the smallest natural frequency at, say, 20.3 Hz. What will happen when the motors excity my structure? This is another type of analysis, this is an harmonic analysis. The answer will require an accurate input of the damping of the structure (low damping ---> high vibration). I will leave to some other user or ANSYS employee to answer how you can input two excitation points, because I never did this. Consider that probably the two excitation will not be in phase.
>>Totally what are the inputs I should apply to get correct natural frequency modes.
again: accurate distribution of the mass (center of gravity for the concentrated masses, correct density for the rest) + correct representation of constraints (be careful to constrain in the exact way the system is constrained in reality, consider that e.g. a bolted connection is not perfectly stiff and so on) + correct represenation fo the stiffness (E-module, all springs correctly represented, other stiffnesses). The excitation has nothing at all to do with natural frequency, they are called so because they are free.
-
February 27, 2023 at 5:17 am
Sankar Krishnan
SubscriberDear Peteroznewman
Kindly tell me the steps to be followed to proceed harmonic analysis of the vibrating structure.
vibrating motor frequency-y hz
creates working moment - X N-m2
vibrating structure is vibrating on springs.
@peteroznewman #peteroznewman
-
- The topic ‘How to find the Natural frequency of Vibrating Structure ?’ is closed to new replies.



-
5274
-
1859
-
1398
-
1257
-
1021

© 2026 Copyright ANSYS, Inc. All rights reserved.