Learning Forum

[Milind Lal]

I have two concentric rings with frictional contact defined between them. There are threads on the outer ring which are symmetric in the quarter section. So when the inner ring rotates, it translates in the axial direction. 

My goal is to study the required force to make the ring rotate and bend the elastic materials present on the inner ring.

I have achieved convergence when I fix the outer ring and provide displacement boundary condition to the inner ring. In this simulation, the force and moment reaction probes were succesfully achieved. 

But when I try to simulate it with tangential force(in cylindrical co-ordinates) or moment as boundary condition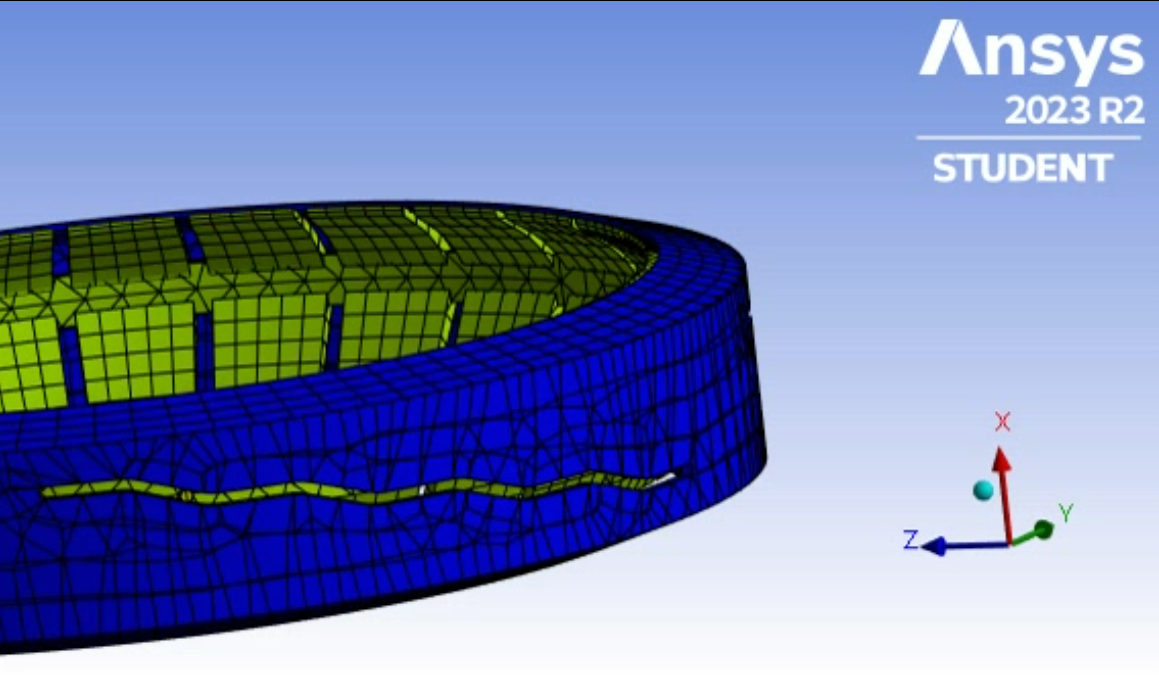, the solver cannot achieve convergence even with NEQIT 100. The solver fails as soon as the inner ring starts moving. Are there any other ways to simulate this problem? 

Due to the mesh limit in student version, I have to use symmetry region and cyclic symmetry for the same. Open to any suggestions. 

[Ashish Khemka]

Hi Milind,

Applying force or moment might lead to rigid body motion and your first approach of applying displacement and then extracting the reaction looks fine.

 

Regards,

Ashish Khemka

[Milind Lal]

How can I avoid rigid body motion and make it converge with force or moment? Solving with displacement is not an option I have.