Calculation of displacement from nodes on the interface of two materials
TAGGED: interface, interface-boundary, structural-mechanics
-
-
October 4, 2021 at 1:49 pm
amit.pandey
SubscriberHello,
I have a very rudimentary question on how the material properties are imparted to the common nodes on an interface between two different materials?
Lets say for example, I have a bimetallic strip. One strip is aluminium and the other is copper.
How will the strain on the nodes at the interface be calculated? If we use strain= alphaXdelta_Temp.... then the alpha to be used in this calculation should be from Aluminium or from copper? Or both?
if both the values are used for calculations, then how is the displacement of the interface evaluated from these strains?
Any inputs are appreciated.
Best regards,
Amit
October 4, 2021 at 2:44 pmgreg2835
SubscriberAssuming the interface is bonded, the strains are calculated based on both alphas and satisfying the internal equilibrium equation. Imagine if you separated both materials and drew a free body diagram. On an element to element basis, equilibrium must be met - which comes from first calculating the strains (including thermal) and then the stresses, and these stresses must satisfy equilibrium as seen below. This is just my two cents, others might have better, more accurate info.
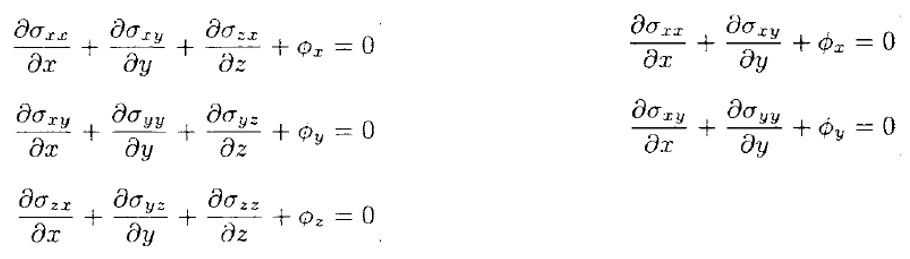
October 4, 2021 at 2:47 pmpeteroznewman
SubscriberThe flow of data in a finite element analysis is the nodes have an unknown displacement, but the elements have known properties of stiffness and thermal expansion. Ansys assembles a stiffness matrix [K] using the known element properties and solves the matrix equation [K]{u} = {F} for the unknown nodal deformations in the {u} vector for the applied loads in the {F} vector. The solution results in all internal forces being in equilibrium with the external applied forces and reaction forces from the constraints.
Once the nodal deformations are known, the strain can be calculated. The strain at the interface between an adjacent pair of nodes is the same for both copper and aluminum, but because those two materials have different values of Young's Modulus (E) the stress in each element will be different. Because of that, you would turn off Nodal Averaging of the Stress Contour plot because there is a discontinuity of stress at the interface, even though there is no discontinuity of deformations.
October 4, 2021 at 4:34 pmRameez_ul_Haq
Subscriber,I would be glad if you could also answer my query in this thread.
You mentioned, "The solution results in all internal forces being in equilibrium with the external applied forces and reaction forces from the constraints.", so I have read that the reaction forces at the boundary conditions are the unknowns, we know this. So basically, the solution to stiffness matrix equation gives us the unknown displacements as well as the unknown forces (at the boundaries), right? Well, to be more exact, the reaction forces from the constraints are going to be in equilibrium with the external applied forces. I just want to understand that the internal forces that you mentioned, are these the forces at the nodes, or within an element? Secondly, if these internal forces are at the nodes, then what are they compared against to check equilibrium? Because the externals are balanced by the forces at constraints. These nodes (which are neither the constraints nor any external forces are applied there), we know that we find the displacements of them by solving the stiffness matrix equation, but how do we find the internal force at these?
October 4, 2021 at 7:36 pmRameez_ul_Haq
Subscriber,please observe the figure below which I got from ANSYS Learning YouTube Channel : https://www.youtube.com/watch?v=FVbXx5Dv4ME&t=28s&ab_channel=AnsysLearning
 So, as written in the 3rd point, the internal forces are calculated by first computing the elemental stresses, and then refinding the forces from it. I am still confused that if the solver tries to find the internal forces at the nodes or within the element. Plus, I couldn't understand that what equation(s) is basically used to find these internal forces from the stresses. It shouldn't be a simple relation like F/A for this, it should be something complex which I don't know.
So, as written in the 3rd point, the internal forces are calculated by first computing the elemental stresses, and then refinding the forces from it. I am still confused that if the solver tries to find the internal forces at the nodes or within the element. Plus, I couldn't understand that what equation(s) is basically used to find these internal forces from the stresses. It shouldn't be a simple relation like F/A for this, it should be something complex which I don't know.
Moreover, I also couldn't understand that how could the solver tell me that in this region locally, the force is not converging. I am talking about if I open NR-Residual plots, then I would be able to see locally in my FEM model that where convergence problem is occurring. I mean for this to happen, then solver should know external as well as internal forces locally there. But there is no external force applied there (for example) and internal is calculated from the stresses (as already mentioned). So how does the NR-Residuals are able to show me the local unconvergence region?
And also, I think the presenter meant to actually write, " ..... to obtain the next approximation of the stiffness matrix" in point 5. What do you think?
I would be glad if you could your views on these queries.
October 4, 2021 at 8:33 pmgreg2835
SubscriberYea I was a bit confused about all this a while ago so maybe I can clear things up a bit. FYI, is right on with his statement which I'm only (attempting) to elaborate on.
So at first the solver assembles the stiffness matrix K, and then solves for F and u. F is only the *external forces* and not at the internal nodes (though it is possible for this to happen but let's keep this simple), and u is the displacement of *all nodes*.
Once the displacements are found the solver can then numerically integrate to get stress and strain at the *Gauss/Integration points*, which are then extrapolated to *all nodes* (don't let this confuse you, just know you ultimately get stress and strain at the nodes). However, the solver also generates a *tangent stiffness matrix* (this is where it might get confusing). This is basically d_stress / d_strain (partial derivatives). When elastic, this is the same as the elastic matrix; but when nonlinear behavior happens this is very useful. Anyway, this new matrix allows you to evaluate *each element* and determine the internal forces for each element. If the residual of the external and internal forces are too large, the solver iterates again until convergence is met.
So yes after solving Ansys knows both the external and internal forces.
Step 5 is talking about the increment for the next NR iteration, which is an update of the *displacement vector*.
There's a bit more going on but hopefully the tangent matrix idea helps.
Edit: added *displacement vector*
October 4, 2021 at 8:50 pmgreg2835
SubscriberI liked this part of the Ansys Mechanical Basic Structural NonLinearities - Module 01 - Practical Considerations on Learning Hub. You get to see the equilibrium iterations between each NR iteration as the solver must converge on equilibrium (balance of internal and external forces) before the next NR iteration occurs.

October 4, 2021 at 8:51 pmpeteroznewman
Subscriber"The solution results in all internal forces being in equilibrium with the external applied forces and reaction forces from the constraints."
I was oversimplifying the flow of data in a finite element analysis. What actually happens there is a complete stiffness matrix that has all nodal degrees of freedom (x, y, z) where most of the deformations are unknown, while at the supports the deformation is known to be zero. The rows and columns with the known zero deformations are eliminated from the complete stiffness matrix. It is the reduced stiffness matrix that is solved for the unknown nodal deformations. Now the known and solved nodal displacements are substituted into the complete stiffness matrix to compute the unknown reaction forces.
The finite element method is based on mathematical methods that result in a matrix equation formulated to minimize the virtual work in the entire domain. That is what it means to be in equilibrium. The solver is not actually balancing forces when it is computing, that is just built into the formulation. You should read that Finite Element Method book I recommended to understand this point.
Since the stiffness matrix represents the stiffness of every node in each direction, and the solution has revealed the deformation of every node in each direction, the force on every node in each direction is known, so it is possible to see the internal forces in the solution.
The above paragraphs describe a single linear solve. Your second post is about nonlinear solution logic, which uses multiple linear solves where things change between each solve to converge on the nonlinear solution. I will address that in a separate reply.
October 5, 2021 at 7:24 amRameez_ul_Haq
Subscriberthank you for your answer sir. Sure, I would be waiting for your second reply as well here.
Secondly, regarding the second last paragraph which you wrote, so it means that the internal forces are basically not at all required beforehand to calculate the displacements of the nodes. They are calculated based on first calculating the nodal displacements, right? I just to be sure about this. Because the basic FEM course I took in my Bachelors Degree, it was taught only about simple beam elements and in order to calculate the unkown nodal displacements, the internal forces at those nodes were already provided.
And yes, I was planning to start reading the book which you recommended by Reddy, but I thought that starting with the basic understanding of the concepts first which are provided on the ANSYS Learning is a better idea before jumping onto the book. So I am trying to complete the basic courses first.
October 5, 2021 at 9:14 amamit.pandey
SubscriberHi Peter
In all the discussion I somehow seemed to miss the most important part.
"The strain at the interface between an adjacent pair of nodes is the same for both copper and aluminum, but because those two materials have different values of Young's Modulus (E) the stress in each element will be different."
Does this mean that the nodes at the interface have the material properties of both aluminium and copper and the deformations based on the matrix evaluation is calculated based on both material properties. Then to satisfy equilibrium, the deformation which corroborates with the equilibrium condition is accepted as the deformation of this node?
And then based on this deformation the strain is calculated and consecutively the stress (which is different for both the material because of the different Young's modulus) is calculated?
Is that what you meant or am I missing something here?
Also, could you please mention the name of the book again? I can not seem to find it in the comment chain.
Best regards Amit
October 5, 2021 at 11:39 ampeteroznewman
SubscriberHi Amit When the stiffness matrix is assembled, a node on the interface picks up information from an element of aluminum and an element of copper, since they share that node. So yes, when the matrix equation is solved, the deformation of that node is based on both materials.
So while a single node can only have a single deformation vector, the element on each side of that node can have different values of stress due to different values of E. As mentioned, a shape function describes the stress at each point in the element, so there are multiple values of stress at a single node. When all the elements sharing a node have the same material, it is useful to average all the stress values of all the elements connected to a node. But when different materials are connected to a node, it is more useful to NOT average the stress values at a node.
The book is mentioned in this discussion: /forum/discussion/comment/133109#Comment_133109
October 5, 2021 at 11:51 ampeteroznewman
SubscriberCorrect, the internal forces are not needed prior to solving for the deformations. They are only known afterward.
When teaching a simplified concept of the finite element method, perhaps your course showed that there must be equilibrium at each node and that requirement was used to derive the stiffness of each element. Equilibrium is also baked into the finite element method of a more complicated mesh of continuum elements, but without reference to any internal forces. As you read the book, there are the partial differential equations which are called the Strong Form of the boundary value problem, but those are too difficult to solve, so the mathematical trick is to integrate those over the domain, and those equations are called the Weak Form of the BVP and those can be solved numerically.
October 5, 2021 at 12:02 pmRameez_ul_Haq
Subscriberthank you for clarifying :) Would be glad to hear your words on this one as well:
October 10, 2021 at 3:38 pmRameez_ul_Haq
Subscriber,can you kindly provide an insight on the previous comment I made for the non-linear analysis. Thank you.
October 10, 2021 at 8:13 pmpeteroznewman
SubscriberI suggest reading in ANSYS Help the Theory Reference, Chapter 14.10 Newton-Raphson Procedure. In 14.10.1 Overview, a restoring load vector {Fnr.i} is computed from the current stress state. This vector is subtracted from the applied load vector {Fa.i} and when the difference between these vectors falls below a convergence tolerance, that substep is considered converged.
October 10, 2021 at 8:30 pmRameez_ul_Haq
Subscriber,sure. Will do that. Thank you for your suggestion :)
Viewing 15 reply threads- You must be logged in to reply to this topic.
Innovation SpaceTrending discussionsTop Contributors-
4683
-
1565
-
1386
-
1242
-
1021
Top Rated Tags© 2025 Copyright ANSYS, Inc. All rights reserved.
Ansys does not support the usage of unauthorized Ansys software. Please visit www.ansys.com to obtain an official distribution.
-











