Ansys Learning Forum › Forums › Discuss Simulation › Photonics › Regarding box of monitors and far field simulations › Reply To: Regarding box of monitors and far field simulations
Hi Prabha,
I have changed the “scat_ff” analysis group so that it can be used correctly with 5 monitors. I added a parameter called “include_sub” which lets you decide if you want to disable the monitor in the substrate. Also, added some if conditions in the Analysis script so that the if there is no substrate, we can use the symmerty conditions depending upon whether or not required. But if it is include_sub is false, the monitor data from “z1” is completely ignored. Before making these changes, even if you disable the monitor, it would consider symmetry conditions and manipulate the values of z1, to get the values of z2. I can not share the files with you directly as ALF doesn’t permit it. But here are the screenshots and code snippets:
- First add “scat_ff” from the Object Library (Far field from a closed box).
- Change it’s span and position (make it same as the previous farfield group).
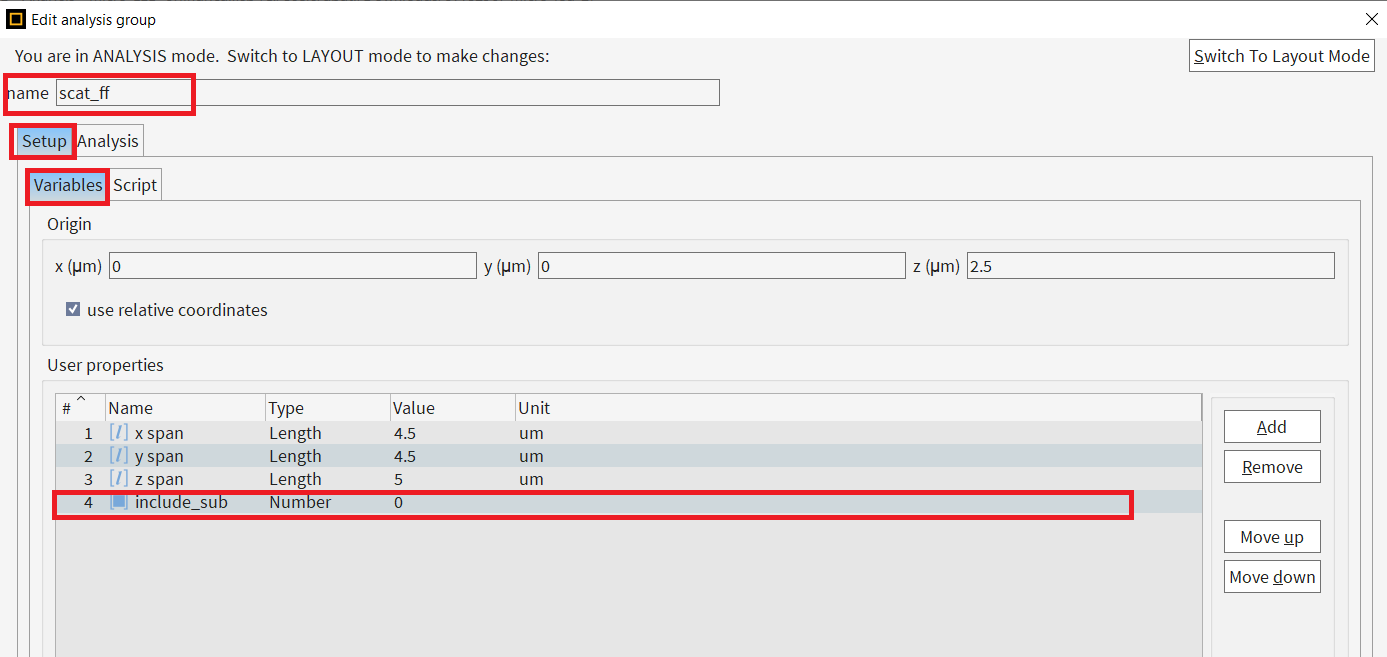
- Edit it, go to “Setup–>Variables“, add a property called "include_sub" of type Number:
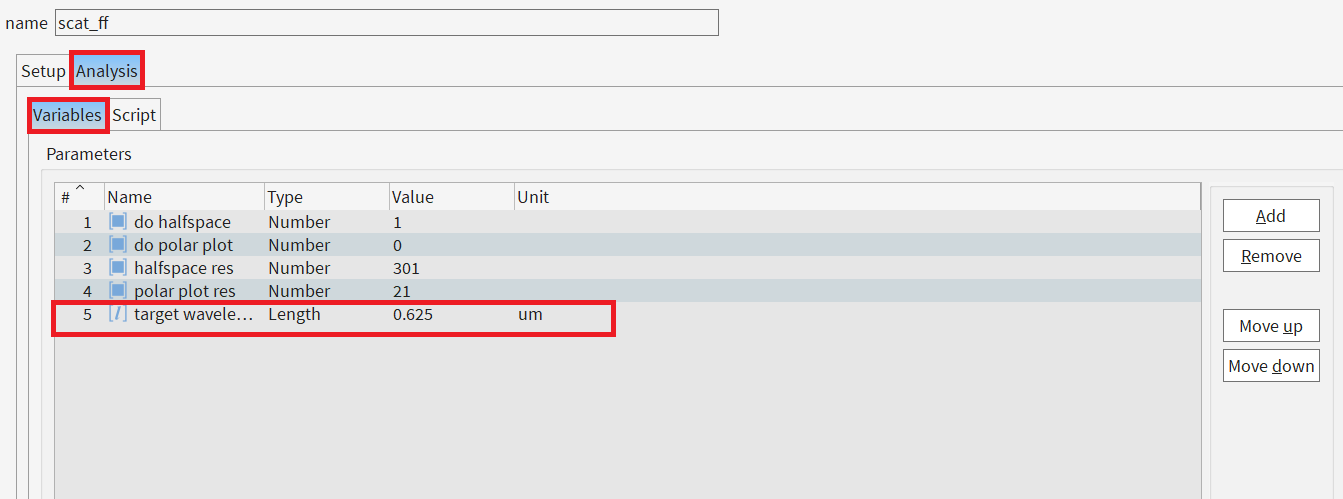
- Go to Setup–>Script, replace the existing code by the following:
##############################################
# Far field from closed box
# This script sets up the monitor box
#
# Input properties
# x,y,z span: span of the box of monitors
#
# Tags: far field projection closed box
#
# Copyright 2012 Lumerical Solutions Inc
##############################################
# simplify variable names by removing spaces
x_span = %x span%;
y_span = %y span%;
z_span = %z span%;
select(“z1”);
set(“x”,0);
set(“x span”,x_span);
set(“y”,0);
set(“y span”,y_span);
set(“z”,-z_span/2);
set(“enabled”,include_sub);
select(“z2”);
set(“x”,0);
set(“x span”,x_span);
set(“y”,0);
set(“y span”,y_span);
set(“z”,z_span/2);
select(“x1”);
set(“x”,-x_span/2);
set(“y”,0);
set(“y span”,y_span);
set(“z”,0);
set(“z span”,z_span);
select(“x2”);
set(“x”,x_span/2);
set(“y”,0);
set(“y span”,y_span);
set(“z”,0);
set(“z span”,z_span);
select(“y1”);
set(“x”,0);
set(“x span”,x_span);
set(“y”,-y_span/2);
set(“z”,0);
set(“z span”,z_span);
select(“y2”);
set(“x”,0);
set(“x span”,x_span);
set(“y”,y_span/2);
set(“z”,0);
set(“z span”,z_span);
select(“index”);
set(“x”,x_span/2);
set(“y”,y_span/2);
set(“z”,0);
set(“x span”,0);
set(“y span”,0);
set(“z span”,0);
5. Go to Analysis–>Script, replace the existing code by the following:
##############################################
# Far field from closed box
# This script calculates scattering cross-section and far field projection in half space
#
# Note: The far field projection calculation assumes that all of the monitors
# are in a single homogeneous material (i.e. there is no substrate)
# If a substrate is present, results from this object will be invalid.
# If multiple frequency points are collected, the projection can be slow!! One could reduce the halfspace resolution for faster analysis.
# For more information, see http://docs.lumerical.com/en/layout_analysis_projections_from_monitor.html
#
# symm x,y,z: symmetry boundary conditions
# 0 for no symmetry, 1 for symmetric, -1 for antisymmetric
# Autodetection is managed by examining fields at the symmetry boundary
# For more information, see http://docs.lumerical.com/en/index.html?ref_sim_obj_symmetric_anti-symmetric.html
#
# do halfspace: Calculate the far field in the full half space for all frequencies. This takes longer than the 1D radar line cross sections. 1 for yes, 0 for no
# do polar plot: Calculate the far field scattering angular distribution for a specified target wavelength. 1 for yes, 0 for no
# target wavelength: Desired wavelength for polar plot. The closest wavelength recorded by the monitors will be found and used for the plot.
# halfspace res: Define the resolution of the half space projection. This will significantly affect the time to run the analysis.
# polar plot res: Define the resolution of the polat plots.
#
# Output properties
# XY, YZ, XZ: E, |E|^2, |H|^2 far field profile of scattered field in plane, as a function of frequency
# XY_halfspace: E, |E|^2, |H|^2 in full upper/lower half space,, as a function of frequency. Similar to standard projection from a single monitor
#
# Tags: far field projection closed box
#
# Copyright 2015 Lumerical Solutions Inc
##############################################
##############################################
# automatically unfold field data if symmetry BC is applied
if (havedata(“x1”, “f”)) {
symm_x = 0;
} else {
xtemp = getdata(“y2”, “x”);
ztemp = getdata(“y2”, “z”);
Eztemp = pinch(getdata(“y2”, “Ez”));
Ez2mid = sum(Eztemp(round(length(xtemp)/2), 1:length(ztemp))^2);
if (Ez2mid != 0) {
symm_x = 1;
} else {
symm_x = -1;
}
}
if (havedata(“y1”, “f”)) {
symm_y = 0;
} else {
ytemp = getdata(“x2”, “y”);
ztemp = getdata(“x2”, “z”);
Eztemp = pinch(getdata(“x2”, “Ez”));
Ez2mid = sum(Eztemp(round(length(ytemp)/2), 1:length(ztemp))^2);
if (Ez2mid != 0) {
symm_y = 1;
} else {
symm_y = -1;
}
}
if(include_sub){
if (havedata(“z1”, “f”)) {
symm_z = 0;
} else {
xtemp = getdata(“y2”, “x”);
ztemp = getdata(“y2”, “z”);
Eytemp = pinch(getdata(“y2”, “Ey”));
Ey2mid = sum(Eytemp(1:length(xtemp), round(length(ztemp)/2))^2);
if (Ey2mid != 0) {
symm_z = 1;
} else {
symm_z = -1;
}
}
}
f = getdata(“x2″,”f”); # get freqency data
if (havedata(“index”,”index_x”)) { # get refractive index. Required to calcualte H2 from E2
n_index = getdata(“index”,”index_x”);
} else {
n_index = getdata(“index”,”index_z”);
}
##############################################
# define the angular resolution
phi = linspace(0,360,%polar plot res%); # user-modifiable in the Variables tab
npts = length(phi);
# define the field data matrices for angular distribution
E_xy = matrix(npts, 3, length(f)); # 3 for x, y, z component
E_yz = matrix(npts, 3, length(f)); # 3 for x, y, z component
E_xz = matrix(npts, 3, length(f)); # 3 for x, y, z component
E2_xy = matrix(npts,length(f));
E2_yz = matrix(npts,length(f));
E2_xz = matrix(npts,length(f));
H2_xy = matrix(npts,length(f));
H2_yz = matrix(npts,length(f));
H2_xz = matrix(npts,length(f));
# Identify the closest wavelength to target:
target_wavelength = %target wavelength%;
i_target = find(f,c/target_wavelength);
?”Target wavelength = ” + num2str(target_wavelength);
?”Wavelength used = ” + num2str(c/f(i_target));
if (havedata(“z2″,”Ex”)) { # have z data, 3D simulation
##############################################
# Angular distribution calculation for a 3D simulation begins
for (i = 1:length(f)){ # loop for all frequencies
# print the frequency point number running in the loop
?”Angular distribution i=”+num2str(i)+”, “+num2str(c/f(i)*1e6)+”um”;
n = n_index(i); # select the frequency point for the index
######## x-y plane (phi=0 corresponds to the direction (1,0,0))
?” Projecting in x-y plane”;
x = cos(phi*pi/180); y = sin(phi*pi/180); z = 0;
# Calculate far field by summing contribution from each monitor
temp = farfieldexact(“x2”,x,y,z,i) + farfieldexact(“y2”,x,y,z,i) + farfieldexact(“z2″,x,y,z,i);
if(havedata(“x1″)){
temp = temp – farfieldexact(“x1″,x,y,z,i);
}else{
temp2 = farfieldexact(“x2″,-x,y,z,i);
s = symm_x*[1,-1,-1];
temp2(1:npts,1) = s(1)*temp2(1:npts,1);
temp2(1:npts,2) = s(2)*temp2(1:npts,2);
temp2(1:npts,3) = s(3)*temp2(1:npts,3);
temp = temp – temp2;
}
if(havedata(“y1″)){
temp = temp – farfieldexact(“y1″,x,y,z,i);
}else{
temp2 = farfieldexact(“y2″,x,-y,z,i);
s = symm_y*[-1,1,-1];
temp2(1:npts,1) = s(1)*temp2(1:npts,1);
temp2(1:npts,2) = s(2)*temp2(1:npts,2);
temp2(1:npts,3) = s(3)*temp2(1:npts,3);
temp = temp – temp2;
}
if(include_sub){
if(havedata(“z1″)){
temp = temp – farfieldexact(“z1″,x,y,z,i);
}else{
temp2 = farfieldexact(“z2″,x,y,-z,i);
s = symm_z*[-1,-1,1];
temp2(1:npts,1) = s(1)*temp2(1:npts,1);
temp2(1:npts,2) = s(2)*temp2(1:npts,2);
temp2(1:npts,3) = s(3)*temp2(1:npts,3);
temp = temp – temp2;
}
}
E_xy (1:length(phi), 1:3, i) = temp;
E2_xy (1:length(phi), i) = sum(abs(temp)^2,2); # E2 = |Ex|^2 + |Ey|^2 + |Ez|^2
H2_xy (1:length(phi), i) = E2_xy (1:length(phi), i) * n^2 * eps0/mu0; # for a plane wave, E^2 and H^2 only differ by a factor of n^2*eps0/mu0
######## y-z plane (phi=0 corresponds to the direction (0,1,0))
?” Projecting in y-z plane”;
x = 0; y = cos(phi*pi/180); z = sin(phi*pi/180);
# Calculate far field by summing contribution from each monitor
temp = farfieldexact(“x2”,x,y,z,i) + farfieldexact(“y2”,x,y,z,i) + farfieldexact(“z2″,x,y,z,i);
if(havedata(“x1″)){
temp = temp – farfieldexact(“x1″,x,y,z,i);
}else{
temp2 = farfieldexact(“x2″,-x,y,z,i);
s = symm_x*[1,-1,-1];
temp2(1:npts,1) = s(1)*temp2(1:npts,1);
temp2(1:npts,2) = s(2)*temp2(1:npts,2);
temp2(1:npts,3) = s(3)*temp2(1:npts,3);
temp = temp – temp2;
}
if(havedata(“y1″)){
temp = temp – farfieldexact(“y1″,x,y,z,i);
}else{
temp2 = farfieldexact(“y2″,x,-y,z,i);
s = symm_y*[-1,1,-1];
temp2(1:npts,1) = s(1)*temp2(1:npts,1);
temp2(1:npts,2) = s(2)*temp2(1:npts,2);
temp2(1:npts,3) = s(3)*temp2(1:npts,3);
temp = temp – temp2;
}
if(include_sub){
if(havedata(“z1″)){
temp = temp – farfieldexact(“z1″,x,y,z,i);
}else{
temp2 = farfieldexact(“z2″,x,y,-z,i);
s = symm_z*[-1,-1,1];
temp2(1:npts,1) = s(1)*temp2(1:npts,1);
temp2(1:npts,2) = s(2)*temp2(1:npts,2);
temp2(1:npts,3) = s(3)*temp2(1:npts,3);
temp = temp – temp2;
}
}
E_yz (1:length(phi), 1:3, i) = temp;
E2_yz (1:length(phi), i) = sum(abs(temp)^2,2); # E2 = |Ex|^2 + |Ey|^2 + |Ez|^2
H2_yz (1:length(phi), i) = E2_yz (1:length(phi), i) * n^2 * eps0/mu0; # for a plane wave, E^2 and H^2 only differ by a factor of n^2*eps0/mu0
######### x-z plane (phi=0 corresponds to the direction (1,0,0))
?” Projecting in x-z plane”;
x = cos(phi*pi/180); y = 0; z = sin(phi*pi/180);
# Calculate far field by summing contribution from each monitor
temp = farfieldexact(“x2”,x,y,z,i) + farfieldexact(“y2”,x,y,z,i) + farfieldexact(“z2″,x,y,z,i);
if(havedata(“x1″)){
temp = temp – farfieldexact(“x1″,x,y,z,i);
}else{
temp2 = farfieldexact(“x2″,-x,y,z,i);
s = symm_x*[1,-1,-1];
temp2(1:npts,1) = s(1)*temp2(1:npts,1);
temp2(1:npts,2) = s(2)*temp2(1:npts,2);
temp2(1:npts,3) = s(3)*temp2(1:npts,3);
temp = temp – temp2;
}
if(havedata(“y1″)){
temp = temp – farfieldexact(“y1″,x,y,z,i);
}else{
temp2 = farfieldexact(“y2″,x,-y,z,i);
s = symm_y*[-1,1,-1];
temp2(1:npts,1) = s(1)*temp2(1:npts,1);
temp2(1:npts,2) = s(2)*temp2(1:npts,2);
temp2(1:npts,3) = s(3)*temp2(1:npts,3);
temp = temp – temp2;
}
if(include_sub){
if(havedata(“z1″)){
temp = temp – farfieldexact(“z1″,x,y,z,i);
}else{
temp2 = farfieldexact(“z2″,x,y,-z,i);
s = symm_z*[-1,-1,1];
temp2(1:npts,1) = s(1)*temp2(1:npts,1);
temp2(1:npts,2) = s(2)*temp2(1:npts,2);
temp2(1:npts,3) = s(3)*temp2(1:npts,3);
temp = temp – temp2;
}
}
E_xz (1:length(phi), 1:3, i) = temp;
E2_xz (1:length(phi), i) = sum(abs(temp)^2,2); # E2 = |Ex|^2 + |Ey|^2 + |Ez|^2
H2_xz (1:length(phi), i) = E2_xz (1:length(phi), i) * n^2 * eps0/mu0; # for a plane wave, E^2 and H^2 only differ by a factor of n^2*eps0/mu0
} # end of the angular distribution for loop
if (%do polar plot%) { # polar plot for target wavelength
polar(phi*pi/180, E2_xy(1:length(phi), i_target), E2_yz(1:length(phi), i_target), E2_xz(1:length(phi), i_target),
”angle (degrees)”, “|E|^2”, “|E|^2 vs angle @ “+num2str(c/f(i_target)*1e6)+”um”);
legend(“xy plane”,”yz plane”,”xz plane”);
} # end of if polar plot
# create datasets for XY, YZ, XZ for angular distribution
XY = matrixdataset(“XY”);
XY.addparameter(“phi”,phi*pi/180.); #phi angle in radians
XY.addparameter(“lambda”,c/f,”f”,f);
XY.addattribute(“E”,pinch(E_xy,2,1),pinch(E_xy,2,2),pinch(E_xy,2,3)); # Ex, Ey, Ez
XY.addattribute(“E2″,E2_xy);
XY.addattribute(“H2″,H2_xy);
YZ = matrixdataset(“YZ”);
YZ.addparameter(“phi”,phi*pi/180.); #phi angle in radians
YZ.addparameter(“lambda”,c/f,”f”,f);
YZ.addattribute(“E”,pinch(E_yz,2,1),pinch(E_yz,2,2),pinch(E_yz,2,3)); # Ex, Ey, Ez
YZ.addattribute(“E2″,E2_yz);
YZ.addattribute(“H2″,H2_yz);
XZ = matrixdataset(“XZ”);
XZ.addparameter(“phi”,phi*pi/180.); #phi angle in radians
XZ.addparameter(“lambda”,c/f,”f”,f);
XZ.addattribute(“E”,pinch(E_xz,2,1),pinch(E_xz,2,2),pinch(E_xz,2,3)); # Ex, Ey, Ez
XZ.addattribute(“E2″,E2_xz);
XZ.addattribute(“H2″,H2_xz);
# end of the angular distribution for a 3D simulation
##############################################
##############################################
# Halfspace calculation for a 3D simulation begins
# calculate the far field in XY upper/lower half space
if (%do halfspace%) {
res = %halfspace res%; # projection resolution, user-modifiable in the Variables tab
u1 = linspace(-1,1,res);
u2 = u1;
X = meshgridx(u1,u2); # These three lines define the orientation of the hemisphere (ie. XY based halfspace)
Y = meshgridy(u1,u2);
Z = sqrt(1-X^2-Y^2);
filter = abs(imag(Z))<=0; # filter out any values outside of hemisphere
filter2=matrix(res,res,length(f)); # same as filter, just for all frequencies
filter3=matrix(res,res,3,length(f)); # same as filter2, just for all frequencies, Ex, Ey, Ez
for (j=1:length(f)){ # just for filter2 and fitler3 for all frequencies
filter2(1:res,1:res,j)=filter;
filter3(1:res,1:res,1,j)=filter; filter3(1:res,1:res,2,j)=filter; filter3(1:res,1:res,3,j)=filter;
}
x = reshape(X,[res^2,1]); # reshape coordinate matrix into a vector. This is the required form for farfieldexact.
y = reshape(Y,[res^2,1]);
z = reshape(Z,[res^2,1]);
x = [x,x]; # Concatenate a 2nd copy of the vector, for the lower half space
y = [y,y];
z = [z,-z];
npts = length(z); # size of position vector
# define halfspace dataset
E_XY_halfspace = matrix (2*res^2,3,length(f));
E2_XY_halfspace = matrix (2*res^2,length(f));
H2_XY_halfspace = matrix (2*res^2,length(f));
for (i = 1 : length(f)) { # loop for all frequency points
?”Projecting in XY upper half space, i=” + num2str(i)+”, “+num2str(c/f(i)*1e6)+”um”;
# Calculate far field by summing contribution from each monitor
temp = farfieldexact(“x2”,x,y,z,i) + farfieldexact(“y2”,x,y,z,i) + farfieldexact(“z2″,x,y,z,i);
if(havedata(“x1″)){
temp = temp – farfieldexact(“x1″,x,y,z,i);
}else{
temp2 = farfieldexact(“x2″,-x,y,z,i);
s = symm_x*[1,-1,-1];
temp2(1:npts,1) = s(1)*temp2(1:npts,1);
temp2(1:npts,2) = s(2)*temp2(1:npts,2);
temp2(1:npts,3) = s(3)*temp2(1:npts,3);
temp = temp – temp2;
}
if(havedata(“y1″)){
temp = temp – farfieldexact(“y1″,x,y,z,i);
}else{
temp2 = farfieldexact(“y2″,x,-y,z,i);
s = symm_y*[-1,1,-1];
temp2(1:npts,1) = s(1)*temp2(1:npts,1);
temp2(1:npts,2) = s(2)*temp2(1:npts,2);
temp2(1:npts,3) = s(3)*temp2(1:npts,3);
temp = temp – temp2;
}
if(include_sub){
if(havedata(“z1″)){
temp = temp – farfieldexact(“z1″,x,y,z,i);
}else{
temp2 = farfieldexact(“z2″,x,y,-z,i);
s = symm_z*[-1,-1,1];
temp2(1:npts,1) = s(1)*temp2(1:npts,1);
temp2(1:npts,2) = s(2)*temp2(1:npts,2);
temp2(1:npts,3) = s(3)*temp2(1:npts,3);
temp = temp – temp2;
}
}
E_XY_halfspace (1:2*res^2,1:3,i) = temp;
E2_XY_halfspace (1:2*res^2,i)= sum(abs(temp)^2,2); # E2 = |Ex|^2 + |Ey|^2 + |Ez|^2
} # end of halfspace for loop
E_XY_upper_halfspace = E_XY_halfspace(1:res^2,1:3,1:length(f)); # separate the upper/lower data
E_XY_lower_halfspace = E_XY_halfspace((res^2+1):(2*res^2),1:3,1:length(f));
E_XY_upper_halfspace = reshape(E_XY_upper_halfspace,[res,res,3,length(f)]); # reshape the data back into a 2D matrix
E_XY_lower_halfspace = reshape(E_XY_lower_halfspace,[res,res,3,length(f)]);
E_XY_upper_halfspace = E_XY_upper_halfspace*filter3; # set all values outside of hemisphere (ie. the corners of the matrices) to zero
E_XY_lower_halfspace = E_XY_lower_halfspace*filter3;
E2_XY_upper_halfspace = E2_XY_halfspace(1:res^2,1:length(f)); # separate the upper/lower data
E2_XY_lower_halfspace = E2_XY_halfspace((res^2+1):(2*res^2),1:length(f));
E2_XY_upper_halfspace = reshape(E2_XY_upper_halfspace,[res,res,length(f)]); # reshape the data back into a 2D matrix
E2_XY_lower_halfspace = reshape(E2_XY_lower_halfspace,[res,res,length(f)]);
E2_XY_upper_halfspace = E2_XY_upper_halfspace*filter2; # set all values outside of hemisphere (ie. the corners of the matrices) to zero
E2_XY_lower_halfspace = E2_XY_lower_halfspace*filter2;
# create halfspace dataset
XY_halfspace = matrixdataset(“XY_halfspace”);
XY_halfspace.addparameter(“ux”,u1);
XY_halfspace.addparameter(“uy”,u2);
XY_halfspace.addparameter(“lambda”,c/f,”f”,f);
XY_halfspace.addattribute(“E_upper”,pinch(E_XY_upper_halfspace,3,1),pinch(E_XY_upper_halfspace,3,2),pinch(E_XY_upper_halfspace,3,3));
XY_halfspace.addattribute(“E_lower”,pinch(E_XY_lower_halfspace,3,1),pinch(E_XY_lower_halfspace,3,2),pinch(E_XY_lower_halfspace,3,3));
XY_halfspace.addattribute(“E2_upper”,E2_XY_upper_halfspace);
XY_halfspace.addattribute(“E2_lower”,E2_XY_lower_halfspace);
XY_halfspace.addattribute(“H2_upper”,E2_XY_upper_halfspace * n^2*eps0/mu0);
XY_halfspace.addattribute(“H2_lower”,E2_XY_lower_halfspace * n^2*eps0/mu0);
}
# end of the halfspace calculation for a 3D simulation
##############################################
# end of 3D
} else {
##############################################
# Angular distribution for a 2D simulation, only for the XY plane
for (i = 1 : length(f)) { # for all frequency points
n = n_index(i); # select the frequency point for the index
# x-y plane (phi=0 corresponds to the direction (0,1,0))
?” Projecting in x-y plane. 2D simulation.”;
x = -sin(phi*pi/180);
y = cos(phi*pi/180);
z = 0;
temp = farfieldexact(“x2”,x,y,i) + farfieldexact(“y2″,x,y,i);
if(havedata(“x1″)){
temp = temp – farfieldexact(“x1″,x,y,i);
}else{
temp2 = farfieldexact(“x2″,-x,y,i);
s = symm_x*[1,-1,-1];
temp2(1:length(phi),1) = s(1)*temp2(1:length(phi),1);
temp2(1:length(phi),2) = s(2)*temp2(1:length(phi),2);
temp2(1:length(phi),3) = s(3)*temp2(1:length(phi),3);
temp = temp – temp2;
}
if(havedata(“y1″)){
temp = temp – farfieldexact(“y1″,x,y,i);
}else{
temp2 = farfieldexact(“y2″,x,-y,i);
s = symm_y*[-1,1,-1];
temp2(1:length(phi),1) = s(1)*temp2(1:length(phi),1);
temp2(1:length(phi),2) = s(2)*temp2(1:length(phi),2);
temp2(1:length(phi),3) = s(3)*temp2(1:length(phi),3);
temp = temp – temp2;
}
E_xy (1:length(phi), 1:3, i) = temp;
E2_xy (1:length(phi), i) = sum(abs(temp)^2,2); # E2 = |Ex|^2 + |Ey|^2 + |Ez|^2
H2_xy (1:length(phi), i) = E2_xy (1:length(phi), i) * n^2 * eps0/mu0; # for a plane wave, E^2 and H^2 only differ by a factor of n^2*eps0/mu0
} # end of for loop 2D
if (%do polar plot%) { # polar plot for target wavelength
polar(phi*pi/180, E2_xy(1:length(phi), i_target), “angle (degrees)”, “|E|^2”, “|E|^2 vs angle @ “+num2str(c/f(i_target)*1e6)+”um”);
legend(“xy plane”);
} # end of if polar plot
# create dataset for XY
XY = matrixdataset(“XY”);
XY.addparameter(“phi”,phi*pi/180.); #phi angle in radians
XY.addparameter(“lambda”,c/f,”f”,f);
XY.addattribute(“E”,pinch(E_xy,2,1),pinch(E_xy,2,2),pinch(E_xy,2,3)); # Ex, Ey, Ez
XY.addattribute(“E2″,E2_xy);
XY.addattribute(“H2″,H2_xy);
} # end of angular distribution for 2D simulation
########################################
6. Contrary to one of the points I previously made, you can perform a broadband simulation and perform the farfield projection over a single target wavelength:
Feel free to let me know if you have any questions.
Regards,
Amrita