“we have a block standing on a plane and if we push it, it will fall” Are you sure about that?
If the coefficient of friction is small or the force is applied low on the block, it will not tip over, it will slide. But I don’t think you meant that it will fall because it slides off the base plate.
Assume the coefficient of friction is high, or you used a Rough contact condition so the block will not slide. Now you can think about using a force to tip over the block. Assume a coordinate frame where Y is up, X is to the right and the origin is on the bottom, left edge of the block, the one the block will rotate about.
“I apply force or displacement to the top edge and push the block.” These create very different analysis results. Let’s first consider applying a force.
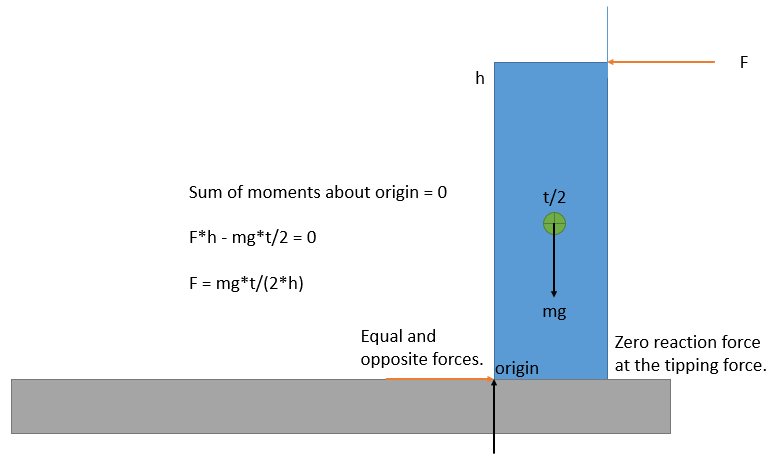
The force that will tip the block over can be calculated by hand. Let’s say the block has a height h, width w and thickness t. Assume a horizontal force F is applied at the top of the block in the -X direction to tip it over. The coordinates of the CG of the block is (t/2, h/2, -w/2).
Calculate the static moment equilibrium about the origin for a constant force F at the top and the weight (mg) of the block acting at the CG. This is the force to tip over the block. At forces less than this, there is a reaction force on both sides of the base. At this force, the reaction force on the right goes to zero. At forces greater than this, the block accelerates as it tips over.
Now consider applying a displacement. For a small displacement, the reaction force at the top will be equal to the tipping force calculated above. As the displacement increases, the force reduces until the force reaches zero when the CG is exactly over the origin. Any displacement more than that will cause the block to tip over. Any displacement less than that is a stable equilibrium and if the displacement returns to zero, the block will return to being supported on its base.
You are navigating away from the AIS Discovery experience