Ansys Learning Forum › Forums › Discuss Simulation › STEM › Effect of Surface Area in Convection in Steady State Thermal Simulation › Reply To: Effect of Surface Area in Convection in Steady State Thermal Simulation
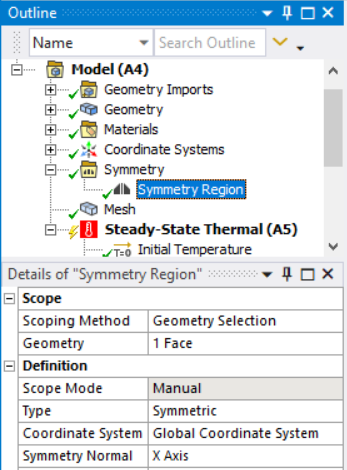
What you describe here is an intention to use a symmetry model. You can insert a symmetry region in the Outline and select a symmetry face(s). Also select the normal axis.
Note that a symmetry condition for heat transfer analysis enforces flux parallel at that face. So you can accomplish the same thing by enforcing a “prefectly insulated” boundary condition at that face. This is the same as enforcing a heat flow of zero at that face.
The reason you get the same answer in your full model and half-model without setting up a symmetry or flux parallel condition is that you probably applied the temperature on the opposite face of the convection, so heat flows straight across, which creates flux parallel conditions at the perimeter faces. Also note that any faces without a load or BC appied and no contact, are considered perfectly insulated faces by default, which is flux parallel.
The heat transfer coefficient (h) in a convection is not macro-geometry dependant. There is no characteristic length for this. That is why there is an area (A) in the convection equation to account for the geometry. You’ll also notice that the h units includes length^2 in the denominator showing that h is a per-area factor, meaning it has factored out model total area. It will depend on micro-geometry such as surface roughness seen under microscope, and the solid and fluid materials involved. This would normally describe natural convection but even forced flow convection can be accounted-for by adjusting h.
An intuitive review of your model would explain that even though the convection area is cut in half in the symmetry model (half the convective heat transfer loss to ambient), with temperature the same on the other side, you still get the same results because you have half the material to heat.