-
-
March 11, 2020 at 1:31 am
mohanpannirselvam08
SubscriberHai I would like to implement this surface intergal equation on a custom plane surface which is situated inside my flow domain.
Equation: D = sum (( v^2 +w^2) *area of cell)
I wiould like to calculate the D (Induced drag) from this wake integral equaition. How can i get the individual cell area of the cell whch the value w and z velocity is taken from. How can i calculate the result of this formula?
-
March 11, 2020 at 2:24 am
Kalyan Goparaju
Ansys EmployeeHello,
You can create a custom field function of your equation using the v and w components of velocity, and cell surface area (in the Adaption category). Once the variable is created, you can use the surface integration from Results → Reports → Surface Integrals -> Edit to sum up the custom variable and get the induced drag.
Thanks,
Kalyan
-
March 11, 2020 at 1:23 pm
mohanpannirselvam08
SubscriberHallo Kalyan Sir,
Thank you for your help.I still not sure where to call up the cell surface area variable from the custom field function. What do you mean Adaption Category?
In the Surface Integrals , does it mean that i dont have to extra define the cell area variable?
For your further refrence i have placed the equation and my domain setting.
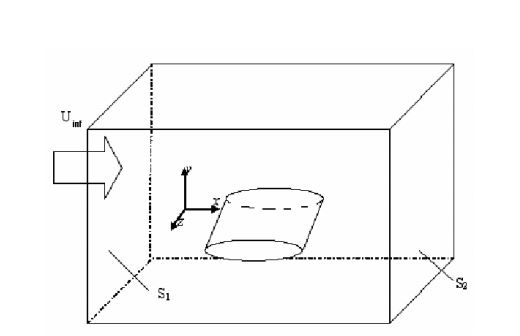
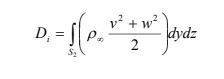
-
March 11, 2020 at 1:52 pm
Kalyan Goparaju
Ansys EmployeeHello,
Sorry for the typo. The cell surface area variable is in the Mesh category and not adaption. Please follow the steps below
1. Before running the simulation, run this command /solve/set/expert no no yes no. This will activate the option of "Keep temporary solver memory from being freed".
2. Run the simulation. Once it is done, go to user-Defined -> Field-Functions->Custom. There, create the variable which is the integrand of your equation. To select the cell surface area, Go to Mesh and then select Cell Surface Area.
3. Once you have the variable, go to Results->Reports->Surface Integrals and pick the appropriate Report Type for the newly created variable, and select the required surface and hit compute.
Thanks,
Kalyan
-
- The topic ‘Surface Integral of a plane’ is closed to new replies.



-
5089
-
1823
-
1387
-
1248
-
1021

© 2026 Copyright ANSYS, Inc. All rights reserved.






