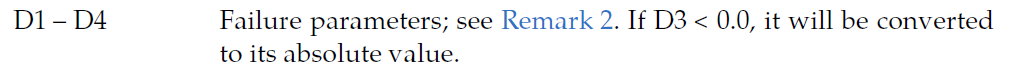TAGGED: ls-dyna, material-properties
-
-
January 26, 2024 at 5:12 pm
rji229
SubscriberHello,
I find that in the LS-DYNA manual 2, the failure parameters are described below:
The D3 will be converted to a positive value if the input is negative. However, in the papers to calculate these parameters, they fit the JC formula and always obtained a negative D3 parameter, such as:
So, I would like to know why LS-DYNA has to convert the negative D3 to its absolute value? Is it because the definition of pressure or effective stress in LS-DYNA is different?
Best,
Rong
-
January 26, 2024 at 8:19 pm
Armin
Ansys EmployeeHi Rong,
Could you include the definition of Johnson-Cook failure criterion from the paper you mentioned above?
It is possible that, in the paper, D3 is multiplied by hydrostatic stress rather than pressure. Pressure is simply the negative of hydrostatic stress and that may explain the difference.-
January 26, 2024 at 9:29 pm
rji229
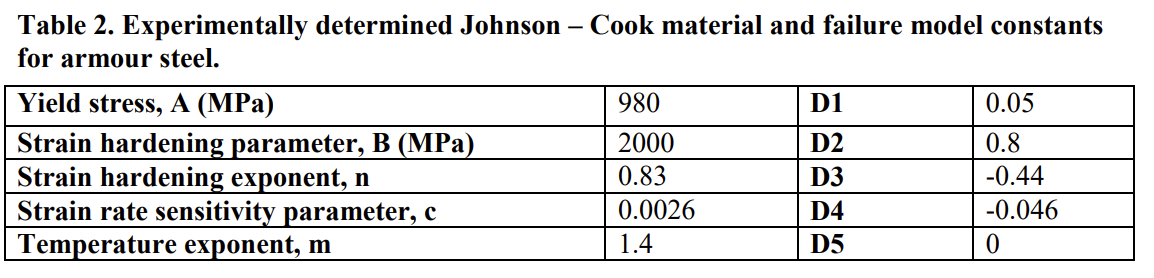
SubscriberThanks for the reply. What I would like to simulate is the AZ31B magnesium alloy. The material parameters are cited from the paper linked: A constitutive and fracture model for AZ31B magnesium alloy in the tensile state - ScienceDirect
The fracture material parameters are defined below:
which are very similar to the formula in LS-DYNA user manual. In real experiment, the parameters are calculated by fitting the data measured, and the result for the paper is shown:
So when using the negative D3 value, we can generate the correct stress-strain curve. However, in LS-DYNA manual, it indicates that D3 must be positive (if negative, use the absolute value). I don't know why we need to do that.
Besides, I also get the same result by using both positive and negative values for the material property for calculation (same absolute value, keeping all other JC parameters the same).
-
-
January 29, 2024 at 4:57 pm
Armin
Ansys EmployeeHi Rong,
Thanks for sharing this. I still think a negative sign might be missing in the definition of stress triaxiality in Equation 4 in your screenshot. Stress triaxiality is commonly defined as the ratio of mean stress (hydrostatic stress) over equivalent stress. Pressure is the negative of hydrostatic stress.
In Johnson-Cook fracture criterion, fracture strain is inversely related to stress triaxiality. In other words, fracture strain should decrease by increasing the stress triaxiality. You can do a few checks using single-element simulation to ensure that the expected fracture trend is resolved in your model.
-
- The topic ‘D3 failure parameter in *MAT_015 (JOHNSON_COOK)’ is closed to new replies.



-
4833
-
1587
-
1386
-
1242
-
1021

© 2026 Copyright ANSYS, Inc. All rights reserved.