-
-
September 18, 2021 at 10:13 am
Urvesh
SubscriberIf I have below geometrical parameteres for 2D Square plate:
L = 0.70 m
G = 68 GPa
Poisson ratio: 0.35
Density: 7.90 g/cm3
Boundary condition: Free from every sides
I need to find the eigenfrequencies using analytical approach..Can anyone give me a formula or procedure how Can I find it?
I have been given solved eigenfrequencies for different values (with same material parameters). Will that be helpful to find new eigenfrequencies with different values?
Hoping to hear from you soon. Thank you
September 18, 2021 at 4:07 pmpeteroznewman
SubscriberYou didn't list the thickness of the plate.
When you say the BC is Free from every side, do you mean the plate is floating in space and has no constraints?
When you say you have to use an analytical approach, do you mean you don't want to perform a Modal analysis in Ansys which numerically calculates the eigenfrequencies? Because that is very easy to do, you only need to increase the number of Modes requested from the default of 6 to 10 or something because the first 6 modes are the numerically zero frequency rigid body modes. The first bending mode is mode 7.
September 18, 2021 at 4:42 pmUrvesh
SubscriberI do not want to perfom it in Ansys workbench. I want to calculate eigenfrequencies by using only analytical approach.
Yes, the plate has no any boundary constraints. As Plate is 2D, thinkness will be ignored I guess. I don't know how to calculate eigenfrequencies by analytical or hand calculations.
September 18, 2021 at 8:49 pmpeteroznewman
SubscriberThickness is a critical input to the calculation because it has a huge effect on the eigenfrequency.
If L = 0.7 m you will get a very different result if t = 0.01 m than if t = 0.001 m
September 18, 2021 at 8:54 pmUrvesh
SubscriberSo do you mean, without the value of Thickness, we cannot find frequencies analytically..right?
If you don't mean this, then what is the analytical approach or formulas to find those frequencies?
Without thickness, we can find frequencies in ANSYS Workbench. The only thing we need to do is convert 2D behaviour of Geometry to 'Plain Strain'. So Ansys workbench does not require Thickness of the geometry.
September 19, 2021 at 4:26 ampeteroznewman
SubscriberWell, 2D has a lot of different meanings and you didn't define it exactly in your original post. Sure, for Plane Strain, there is no need to define thickness. Why are you interested in the eigenfrequencies for a plane strain condition? How is that relevant to any real world application?
September 19, 2021 at 6:57 amUrvesh
SubscriberI have defined all things which I have in my project questions. I could not find the formulas or any source by which I can find analytical solution. Without using thikness and by using parameters defined above by me, Can you calculate frequency?
September 19, 2021 at 12:44 pmpeteroznewman
SubscriberI also could not find a formula, since no one needs this formula in the real world, which is probably why the professor set this as the project question! Maybe the professor wants you to derive the formula yourself from the governing equation that define the eigenvalue problem.
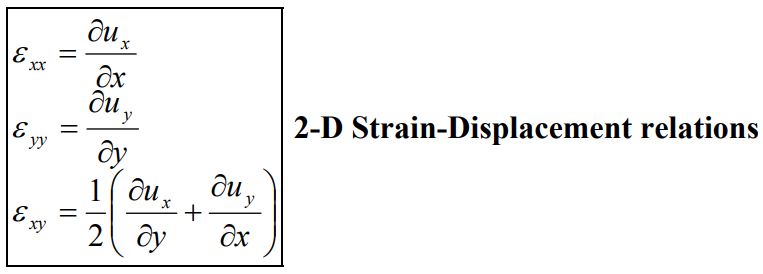
Below are the differential equations relating the stresses and body forces (equations of motion), the strains and displacements (strain-displacement relations) and the strains with each other (compatibility relations) and Hooke's Law (stress-strain relations).
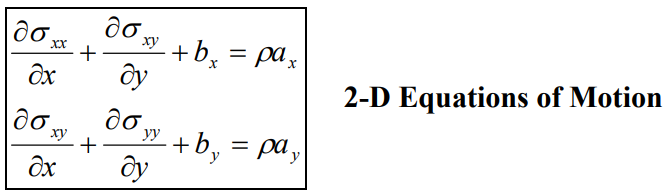 In your case, the body forces b are zero in the equation above.
In your case, the body forces b are zero in the equation above.
 The last set of equations is Hooke's Law for linear isotropic elasticity which use Young's Modulus and Poisson's Ratio to relate stress to strain. You only need three of these six equations depending on whether you are trying to eliminate stress or strain from the above equations.
The last set of equations is Hooke's Law for linear isotropic elasticity which use Young's Modulus and Poisson's Ratio to relate stress to strain. You only need three of these six equations depending on whether you are trying to eliminate stress or strain from the above equations.
 These nine equations, applied to the square domain of length L, together with the boundary conditions, will be used to write the eigenvalue equation. This is the analytical approach, enjoy!
These nine equations, applied to the square domain of length L, together with the boundary conditions, will be used to write the eigenvalue equation. This is the analytical approach, enjoy!
September 26, 2021 at 7:03 pmRameez_ul_Haq
Subscriber,can you tell that these partial differential equations which you have shared (and which I also learned in my Elasticity class) are the ones which are numerically solved in ANSYS? I have heard many times by you that the ANSYS solves partial differential equations, and some integrals must also be done by the solver numerically. I could never actually grasp that what kind of partial differential equations are solved in ANSYS and what integrals are done, and are they done in both linear and non-linear analysis? Numerical approximation is done to solve these partial differential equations and integrals?
And if yes, where exactly are they solved? To compute the stiffness matrix or somewhere else?
September 26, 2021 at 7:45 pmRameez_ul_Haq
Subscriber,and also, you said that the first 6 modes are rigid body modes when there are no supports applied to the model, so the natural frequencies should be zero in these first 6 modes. And we should be concerned about the 7th mode and so on. Why is that so? I mean why are the first 6 modes have a zero natural frequency when there is no supports applied to the structure?
September 26, 2021 at 10:00 pmpeteroznewman
SubscriberTo answer your first post, I suggest you read a book on the Finite Element Method. The book I read in my Masters course was Reddy, An Introduction to the Finite Element Method and it starts with the governing equations, derives the numerical approximations, and ends with computer code to implement it.
To answer your second post, a rigid body has six degrees of freedom, three translations and three rotations. In a static structural model, you need to constrain all six degrees of freedom or there is no solution. If one of the DOF is unconstrained, that means there is zero stiffness in that direction. A natural frequency is sqrt(k/m). If k is zero the frequency is zero. If the rigid body has no constraints, there are six zero frequency modes.
September 27, 2021 at 6:09 amErKo
Ansys EmployeeToo add to what said, there is an nice and open free course on the edx platform that goes though the theory and which I would recommend :
Finally, we do have a theory section in the apdl help manual (chapter 2). Of course we can not expand on that (so if someone can not find something there, we can not provide additional comments), so we can only refer to that theory section. But still perhaps it is a useful reference for users.
As for the rigid body modes, they come out when solving the eigenvalue problem - this example illustrates that:
Thank you
Erik
September 27, 2021 at 6:51 amRameez_ul_Haq
Subscriber, thanks to both of you :)
September 27, 2021 at 11:06 ampeteroznewman
Subscriberand I second Erik's recommendation on the edx.org course. I took that course before this site was launched. It was my first opportunity to solve a Thermal problem and learn CFD. I enjoyed the course, especially helping to answer student questions, that I went through the course a second time just to do that. Professor Bhaskaran recognized me for answering so many questions that he made me a TA on the site so my posts were labeled that way instead of just being a student. He even sent me a Cornell Engineering tee-shirt! But the best thing he did was tell me that Ansys had created a Student Community and that I might enjoy answering questions there. That was how I joined this site so early, which was later renamed the Forum.
September 27, 2021 at 11:44 amErKo
Ansys Employeethanks for sharing that - very nice.
PS: I have aslo taken the course (CFD part mostly) - it is a nice on an appropriate level where both theoretical (on an appropriate level) and practical aspects covered.
November 1, 2021 at 8:15 pmRameez_ul_Haq
Subscriber,since you have already mentioned about the Hooke's Law in this thread. I will try to pitch in a question here.
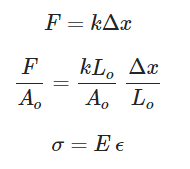 Since the general Stress-Strain relation can be derived from the Hooke's Law (which actually relates the force to displacement with a constant of proprtionality i.e. stiffness or K), so this general Stress-Strain relation should also hold if I am considering a change in stiffness of the structure during deformation of it? [For instance, a fishing rod which encounters a change in its stiffness when it deforms].
Since the general Stress-Strain relation can be derived from the Hooke's Law (which actually relates the force to displacement with a constant of proprtionality i.e. stiffness or K), so this general Stress-Strain relation should also hold if I am considering a change in stiffness of the structure during deformation of it? [For instance, a fishing rod which encounters a change in its stiffness when it deforms].
November 1, 2021 at 9:32 pmpeteroznewman
SubscriberHooke's Law describes a linear relationship so is valid on linear models. Stiffness doesn't change in linear models.
Once you talk about nonlinear effects, then Hooke's law only applies during the initial linear elastic deformation, and not when the large deflection starts. If you have a hyperelastic material model, Hooke's law does not apply because the force-extension data is not linear.
November 1, 2021 at 9:51 pmRameez_ul_Haq
Subscriber,I am just mentioning a fishing rod, or maybe a very thin beam which can bend long way (which changes its stiffness during deformation) when subjected to forces, and still stay below the yield point. I should use Large deflection to take into account the varying stiffness of the structure. But the Stress-Strain relation can be derived from the Force-displacement relation, as I already have shown in the attached picture. However, the stress-strain relation is still kept linear (with constants like E and v) even when I am taking into account the change in stiffness of the structure during deformation. This thing confuses me. I mean for Large Deflection = ON, if we are not using a linear relation to calcuate the stresses from strains in FEM like ANSYS, then it is understandable. But still if we are, then it doesn't make any sense near me because it can be derived from the F = Kx (where K is changable) as written in various textbooks.
"Once you talk about nonlinear effects, then Hooke's law only applies during the initial linear elastic deformation, and not when the large deflection starts.", this statement appeals as if Large deformation should be used after the yield the point, and should not be used before it.
November 1, 2021 at 10:01 pmpeteroznewman
SubscriberTurning on Large Deflection causes the solution to take more time, that is why it is off by default, allowing linear models to solve in the minimum time.
In the fishing rod example, the material remains linear, so on a local scale, Hooke's Law is valid, but at the overall level of the strucure, Hooke's law applied to the rod as a whole is violated because the force-deflection curve does not remain linear at a large deflection.
Any time Plasticity is included in the model so that the material will respond differently after the yield stress is reached should have Large Deflection turned on.
November 2, 2021 at 8:05 amRameez_ul_Haq
Subscriber,I couldn't understand what you mean by saying that Hooke's law is valid on local scale since the material remains linear. What do you mean by local scale? And you also said that for the global structure, Hooke's law is not valid if force-displacement curve is not linear when Large Deflection = ON. If is not valid on a global scale, then how can it be valid for a local scale?
So what does ANSYS consider? Does ANSYS consider a linear relation between stress-strain (i.e. Hooke's law) to calculate the stresses from strains within an element, or it does not and uses some other formulation to do so when Large Deflection is turned ON?
November 3, 2021 at 7:03 pmRameez_ul_Haq
Subscriber,can you please share your thoughts on the comment I made here? Thank you.
November 3, 2021 at 8:55 pmpeteroznewman
SubscriberANSYS computes a global result for the structure. During the solution, each element has local conditions so material yield is evaluated on a local scale within the element. In the fishing rod example, the material remains in the linear range of the stress-strain curve. But when you plot the tip force vs. displacement results, you will find that it is not a straight line.
November 4, 2021 at 7:15 amRameez_ul_Haq
Subscriber,so what you are saying is that on a local scale (i.e. element by element), I can use the linear relationship [as provided in Generalized Hooke's Law] to get stresses from strains, but if I were to use this linear relationship to calculate the stresses from strains not on element by element basis, but instead on a continous global body then it is invalid since the stiffness of the structure on global scale is changing while deforming? Am I correct, sir?
Or it doesn't matter if the stiffness is changing or not during the deformation, since after coming into equilibrium, the stiffness remains constant and that is when we employ the linear relation between stress-strain to calculate the stresses from strains?
November 4, 2021 at 9:52 pmpeteroznewman
SubscriberYes, on an element-by-element basis, the material response is linear. The stiffness of each element is linear.
But on the global scale of the entire structure, the force is not linear with tip displacement because the stiffness of the structure is a function of tip displacement caused by large rotation of the elements.
The reason is that the elements experience a large rigid body deflection (and large rotation) from their initial coordinates. This is large deflection nonlinearity. But the local deformation of each element remains linear.
November 5, 2021 at 6:42 amRameez_ul_Haq
Subscriber,"But the local deformation of each element remains linear.", with respect to the local forces acting on that element, right?
So it basically means that we can always use the linear generalized Hooke's Law for a local element, unless it enters the plasticity phase. Global stiffness varies during deformation, doesn't matter. But for a local element, we still assume the stiffness is linear and is not changing during deformation.
It might be a naive question but it is a little bit confusing that how could the overall structure on the global scale have a non-linear relationship between the force and displacement but the local displacement response of each and every element when subjected to boundary forces (on its nodes) must still remain linear [and thus, we can employ the linear Hooke's law to find the stresses from strains within that element]. I mean the global structure is a composition of local elements, so if global displacement response to force is not linear then doesn't it make sense that the local elements (somewhere within the structure) must also have a non-linear force-displacement relation?
November 5, 2021 at 11:25 amRameez_ul_Haq
Subscriber,so I asked a question related to our discussion on an engineering forum (whose link i am attaching below). You might be interested in having a look at the answers to it.
https://engineering.stackexchange.com/questions/48071/should-we-use-hookes-law-that-linearly-relates-stresses-to-strains-if-the-sti
November 5, 2021 at 11:00 pmpeteroznewman
SubscriberHooke's law says the force is linear with the displacement, but that only works when the force and the displacement remain in alignment. You can have a long thin cantilever and if the tip force is axial, the global force vs displacement curve will be linear.
Rotate that force 90 degrees so the tip force is causing bending in the beam. As the tip rotation increases, the elements rotate, and the direction of the force changes from a bending force and goes toward an axial force, especially for the elements near the tip. Also, as the tip foreshortens and moves closer to the base, the bending moment on the elements at the base is reduced. Both of these changes increase the apparent stiffness of the global structure, but no material stiffness had to change, it is purely a result of large deflection and large rotation. That is why it is called geometric nonlinearity.
November 7, 2021 at 9:15 pmRameez_ul_Haq
Subscriberthank you for your elaborative comment.
I would like to ask something here. For a small deflection of a simple I beam (for instance), we know that we can calculate the deflections and stresses analytically by using Bernoulli-Beam thoery (ofcourse, by keeping in mind the limitations and assumptions made by it), and the results will be exactly the same (ofcourse, by ignoring the numerical errors) as we retrieve from the FEA like ANSYS with Large Deflection OFF. Now, if I want to keep track of the stiffness change during the deformation, so is there any anaytical approach (similar to a Bernoulli-Beam theory) that could be adopted to analytically calculate the displacements and stresses for an I beam, or the only option is using the FEA solvers?
November 7, 2021 at 10:15 pmpeteroznewman
SubscriberThe beam elements used in ANSYS use Timoshenko beam theory that includes shear deformation, which Bernoulli beam theory does not.
For small deflection of a beam, there is no change in stiffness with displacement.
For large deflection of a beam, here is a list of search results for analytical methods of cantilever beams:
https://www.google.com/search?q=analytical+equation+for+large+deflection+of+cantilever+beam
Viewing 28 reply threads- The topic ‘How to calculate eigen frequencies using analytical approach?’ is closed to new replies.
Innovation SpaceTrending discussionsTop Contributors-
4838
-
1587
-
1386
-
1242
-
1021
Top Rated Tags© 2026 Copyright ANSYS, Inc. All rights reserved.
Ansys does not support the usage of unauthorized Ansys software. Please visit www.ansys.com to obtain an official distribution.
-


Ansys Assistant

Welcome to Ansys Assistant!
An AI-based virtual assistant for active Ansys Academic Customers. Please login using your university issued email address.
Hey there, you are quite inquisitive! You have hit your hourly question limit. Please retry after '10' minutes. For questions, please reach out to ansyslearn@ansys.com.
RETRY







