The Ansys Innovation Space website recently experienced a database corruption issue. While service has been restored there appears to have been some data loss from November 13. We are still investigating and apologize for any issues our users may have as a result.
Vibration of Continuous Systems
This learning track covers a comprehensive understanding of vibration problems in dynamic systems, starting with the fundamentals of vibration analysis and the difference between discrete and continuous systems. It delves into the characteristics of dynamic systems, the modeling of undamped and damp systems, and the effects of vibration, such as resonance, fatigue, and serviceability. The track further explores the mathematical properties of periodic functions, the concept of degrees of freedom, and the response of a system subjected to arbitrary excitation. It also discusses the application of transform techniques in solving dynamic systems, and the use of integral transform, particularly Laplace and Fourier transforms, in vibration analysis of linear systems. The learning track then moves on to the study of one-dimensional wave equations, axial and torsional vibrations, transverse vibration in beams, and the force vibration analysis of the Euler-Bernoulli beam. It also covers the vibration in continuous systems, the vibration of membranes and rectangular plates, and advanced vibration analysis techniques. The track concludes with lessons on support excitation in structures, the application of numerical methods in solving dynamic equations, and the spectral method of analysis for structures subjected to random excitation.
These courses has been developed by Prof. Sudip Talukdar from IIT Guwahati for NPTEL. It is now accessible through Ansys Innovation Space courtesy of the partnership between Ansys and NPTEL, under the CC BY-SA license. For more details, visit https://nptel.ac.in/courses/105103221.
1
Innovation Course
Understanding Vibration in Dynamic Systems
This course covers the fundamentals of vibration problems in dynamic systems, focusing on continuous modeling. It explains the difference between discrete and continuous systems, the characteristics of dynamic systems, and the modeling of undamped and da...Read more
2
Innovation Course
Vibration Analysis and Dynamic Systems Principles
This course covers the fundamental principles of vibration analysis and dynamic systems. It starts with the basics of vibration analysis, including the formulation of differential equations for discrete and continuous systems, and the application ...Read more
3
Innovation Course
One-Dimensional Wave Equations
This course covers the comprehensive understanding of one-dimensional wave equations. It begins with the derivation of the wave equation using three different approaches: the discrete approach, the continuum approach using Newton's second law, and Hamilton's equatio...Read more
4
Innovation Course
Axial and Torsional Vibrations
This course covers the comprehensive understanding of axial and torsional vibrations. It begins with the fundamental concept of axial vibration of bars, explaining the derivation of the equation of motion using Newton's Second Law and the energy principle. The cours...Read more
5
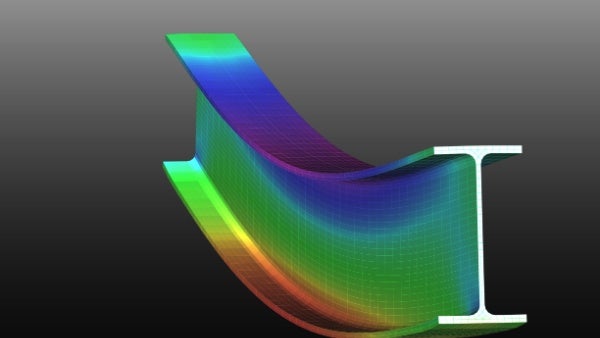
Innovation Course
Transverse Vibration Analysis in Beams
This course covers the comprehensive understanding of transverse vibration in beams, a key component of structural dynamics. It begins with an exploration of various beam theories such as Euler Bernoulli, Release, Shear, and Timoshenko, along with their assu...Read more
6
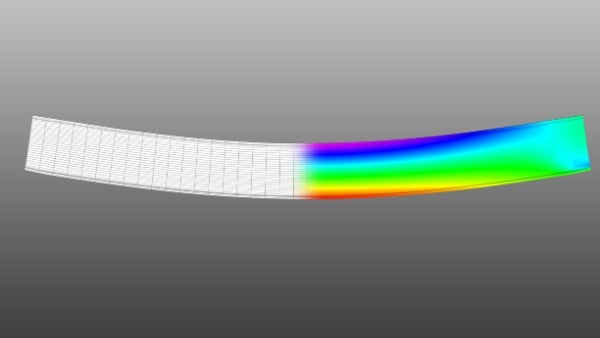
Innovation Course
Advanced Vibration Analysis of Euler-Bernoulli Beams
This course covers the comprehensive study of the Euler-Bernoulli beam's force vibration analysis, a model extensively utilized in diverse engineering applications. The course starts with the general formulation of forced vibration problems and...Read more
7
Innovation Course
Vibration in Continuous Systems
This course covers the comprehensive understanding of vibration in continuous systems. It starts with the exploration of the impact of concentrated masses on the natural frequency of a beam. The course then delves into the analytical solution of a continuous system...Read more
8
Innovation Course
Understanding Vibration of Membranes
This course covers the comprehensive study of the vibration of membranes, both rectangular and circular, and their applications in various fields. The course begins with an introduction to membranes and their significance in engineering and human anatomy. For ...Read more
9
Innovation Course
Vibration Analysis of Rectangular Plates
This course covers the comprehensive study of the vibration of rectangular plates. It begins with the theory of thin plate vibration, discussing the assumptions, derivation of the equation of motion, and the significance of strain, stress, and deflection. ...Read more
10
Innovation Course
Advanced Vibration Analysis Techniques
This course covers three critical lessons on advanced vibration analysis techniques. The first lesson delves into the concept of approximate approaches for vibration analysis, focusing on the release method. It provides an understanding of how this method ca...Read more
11
Innovation Course
Support Excitation in Structures
This course covers the comprehensive understanding of support excitation in structures and its impact on various systems. It begins with the exploration of how forces are induced in a structure due to the displacement of the base, using real-life examples such as ...Read more
12
Innovation Course
Numerical Methods in Dynamic System Analysis
This course covers the application of numerical methods in solving dynamic equations, with a focus on the Duhamel Integral and direct integration methods. It begins with an understanding of the Duhamel Integral and its role in determining the response ...Read more
There is no badge available for this learning track.
Please visit Guided Learning Paths to browse through our selection of other learning tracks.