Response Surface — Lesson 6
In this step, the software builds a surface by interpolating the discrete sampling points selected in the previous step. This can be thought of as building a model of the terrain in the design space.
Start by double clicking on Response Surface in the Project Schematic window. Once the Response Surface window opens click Update. After the update has completed click on Response to see a plot of the volume as a function of hole radius.
Note: Don't worry if you are using a newer version of Ansys Mechanical and your results don't quite match the results shown here. In version 2019 R2, we found the maximum von Mises stress to vary between 32.39 ksi and 34.22 ksi for the given input parameters, instead of between 31.91 ksi and 34.16 ksi as shown here. The differences are insignificant.
Volume
The first plot that appears show the volume of the quarter plate as a function of the hole radius, and is shown below.
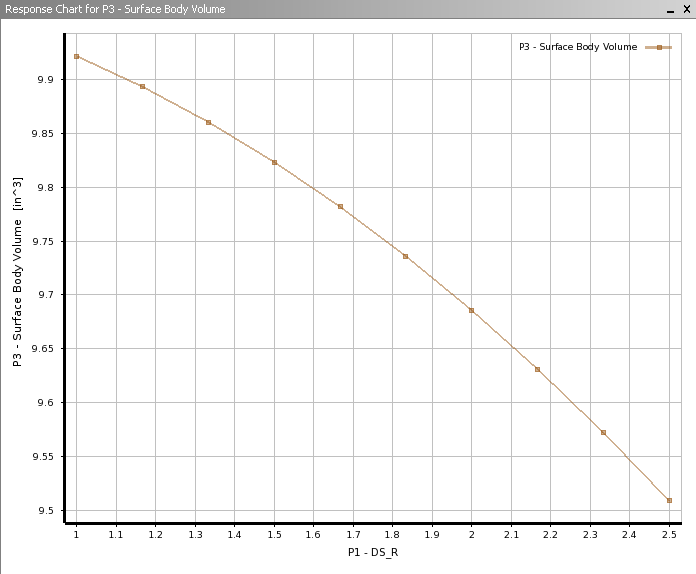
The relation between radius and volume is quite trivial to compute. It will simply be the area of the surface multiplied by the thickness of the surface. With this in mind, V=t*(h*w-(1/4)*pi*r^2) where V=volume, t=thickness, h=height, w=width and r=radius.
Maximum von Mises Stress
To display a plot of the maximum von Mises stress as a function of the hole radius, change the value assigned to Y axis to P3-Equivalent (von-Mises) Stress Maximum. The plot below shows the maximum von Mises stress as a function of the hole radius.
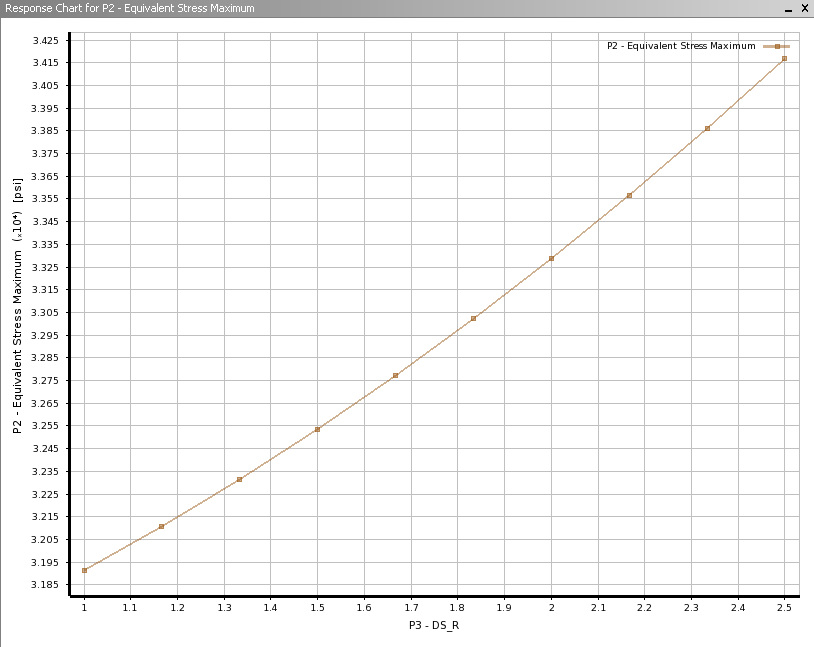
As expected, the maximum von Mises Stress increases as the radius increases. You can use this graph to get an idea of what radius might constitute the upper limit in accordance with our constraint of 32.5 ksi. Remember that to minimize volume, you want the greatest radius possible that still creates an equivalent von Mises stress under our constraint. Taking a close look will tell you that you should expect an optimal radius of around 1.5 inches.
At this point, click Return To Project and then save the project.

