Turbulent Results — Lesson 6
Plot the axial velocity of the turbulent jet at the centerline by going to Plots - XY Plot and click "Set Up." Select the options as in the dialogue below. Make sure to select the centerline surface under Surfaces.

The centerline axial velocity should look like this:
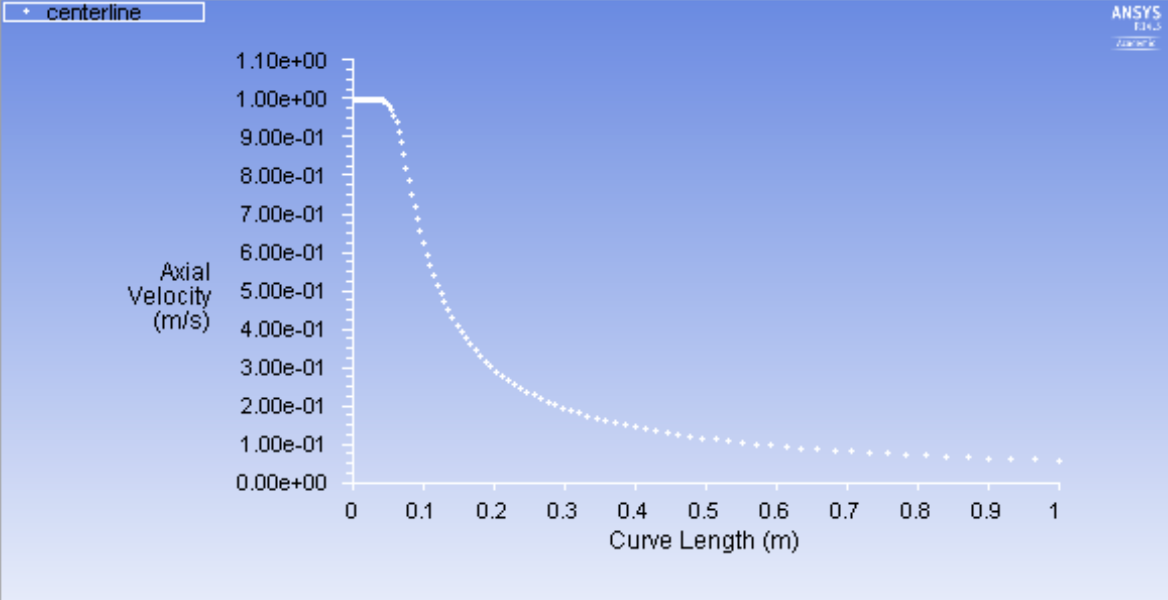
It is clear that the axial velocity decreases with increasing distance from the jet. However, comparing this plot to the centerline velocity in the laminar case, the turbulent case has an initial development region, where the velocity takes a longer distance to start decaying.
Similarly, create a plot of the turbulent kinetic energy k along the centerline: adjust the XY Plot dialogue box to have Y axis function Turbulence - Turbulent kinetic energy (k). The plot is below.
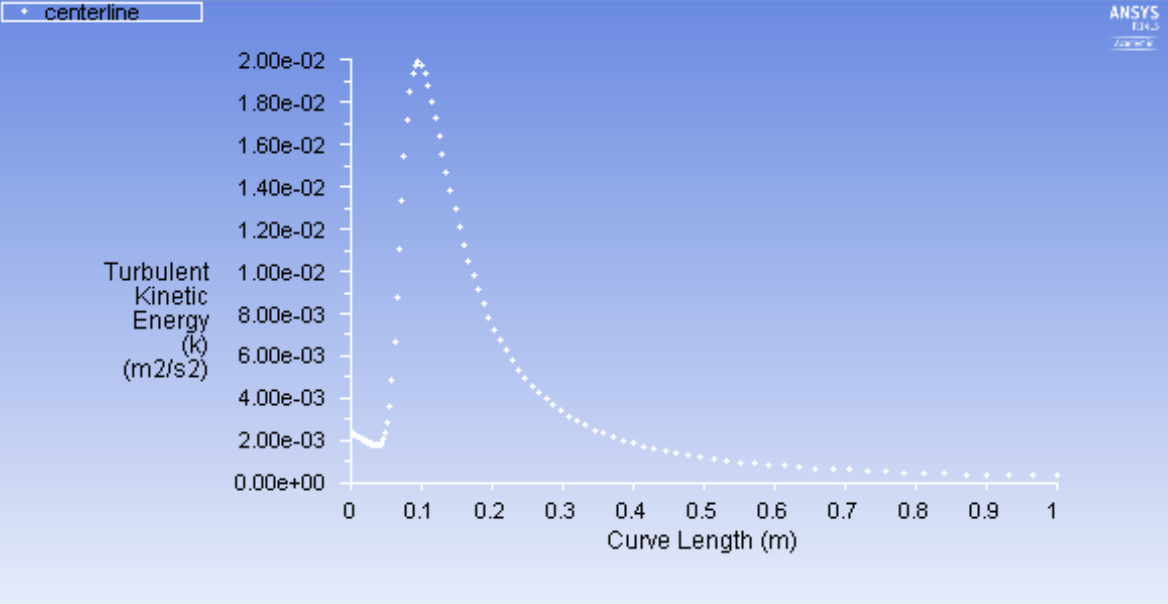
The turbulent kinetic energy is the mean kinetic energy per unit mass in the fluctuating velocity field. It is governed by a production term P, a dissipation term -ε, mean flow convection -Dk/Dt, and turbulent transport -grad(T). The peak in turbulent kinetic energy just after the inlet is due to the production term (affected by fluid shear or friction) dominating; the turbulent kinetic energy again approaches zero as the distance from the inlet increases as the fluid is convected and dissipated away from the centerline into the surroundings.
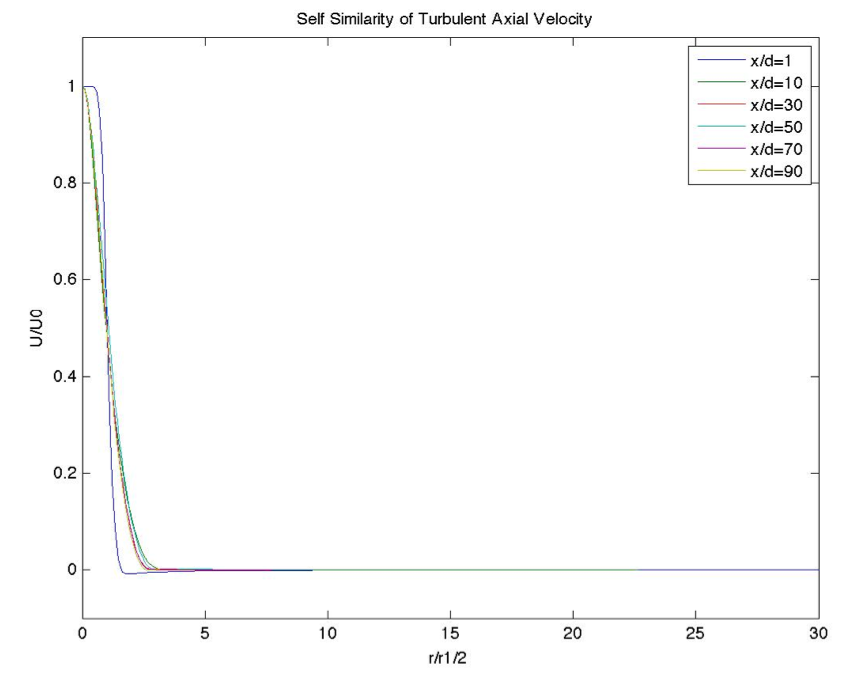
Again, use Matlab or Excel to plot the half width and self-similar profiles U/U_center at various X locations, using exported data as is done in the Laminar Results section. This analysis is intended for more advanced users; if you do not have Matlab, read through the results and skip to the next section.
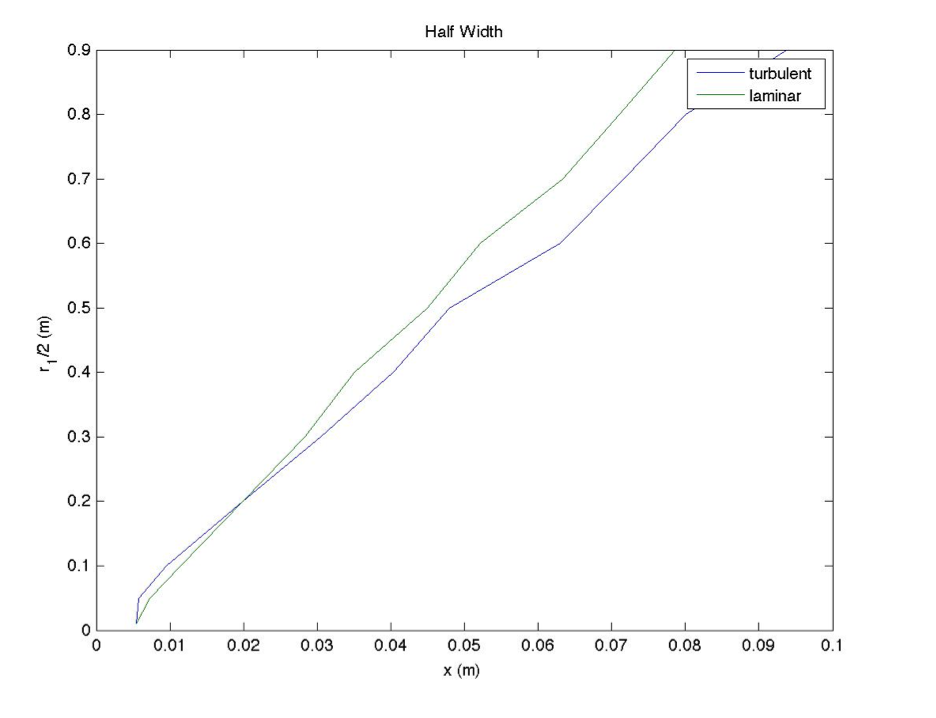
The half width graph with both the laminar case and the turbulent case is below. The turbulent case half width has a longer length scale than the analogous laminar case.
Plots of the axial and radial velocities (scaled by the centerline velocity) vs radial distance from the centerline (scaled by the half width) are below.