Learning Forum

[tarek.azzouni]

Dear community, 
I would like to address, if one of you had the problem for an underestimation of the Bulge stress after constructing his Yield Curve for the material model. during our experiment we noticed that our stress is going at 600MPa at 0.5 strain, therefore, after the Plastic Energy per Volume function our stress droped and now when we try to validate our material using a machine we noticed that the Force is being under estimated by a factor 15-20% 

how is that possible and how can i avoid it ?

Best regards 

[Armin]

Hi Tarek,
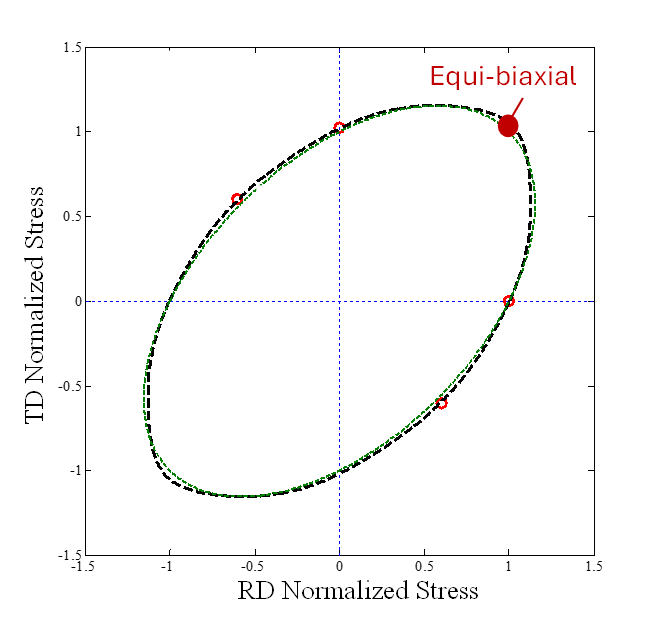
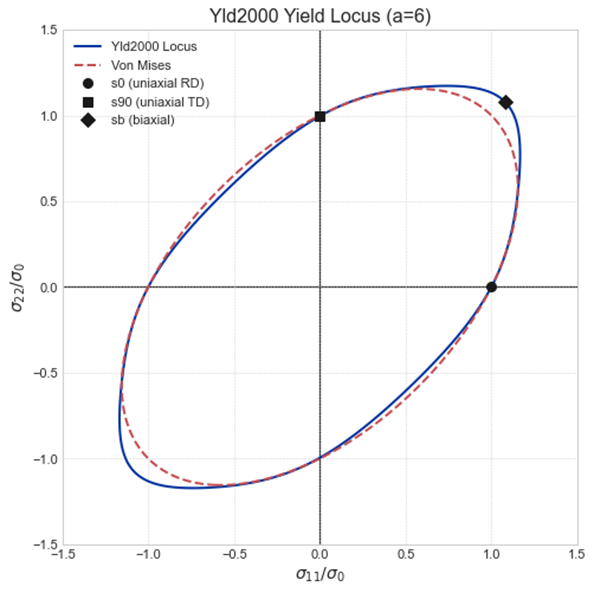
Have you used the equi-biaxial yield stress for the calibration of the Yld2000 model along with other experimental data (such as uniaxial tensile and shear tests)? How does the yield surface prediction compare to the experimental data for equi-biaxial stress (refer to the plot below)? If you have similar plots of yield loci considering experimental data, shown with red symbols below, it would be helpful to compare the goodness of fit of the yield function. Note that the bulge test is known to activate an equi-biaxial stress state, so it is important to have a good fit in the biaxial region to resolve the experimental force-displacement without any over or under predictions. 

[tarek.azzouni]

That's true, I had some difficulties getting the right values. What would you recommend to calculate it sufficiently ? 

[Armin]

Thanks for sharing the plots. I can see that you have a close agreement with the experimental data (sb biaxial) in the yield function fit. The force-displacement response is also captured very well at small displacements. Did you calibrate the Yld2000 yield function at the onset of plastic deformation? If so, you may consider calibrating it at a larger plastic strain (or plastic work), since it appears that there might be evolutions (shape changes) in your yield function with plastic strains. Also, check your hardening curve (input stress-plastic strain data) to ensure that you cover a sufficient range of plastic deformation. If the hardening curve was obtained from a standard dogbone uniaxial tensile test, it may not provide a sufficient range of deformation experienced in bulge tests due to the onset of necking occurring at small strains in dogbone tensile tests.

[tarek.azzouni]

Dear Armin, 
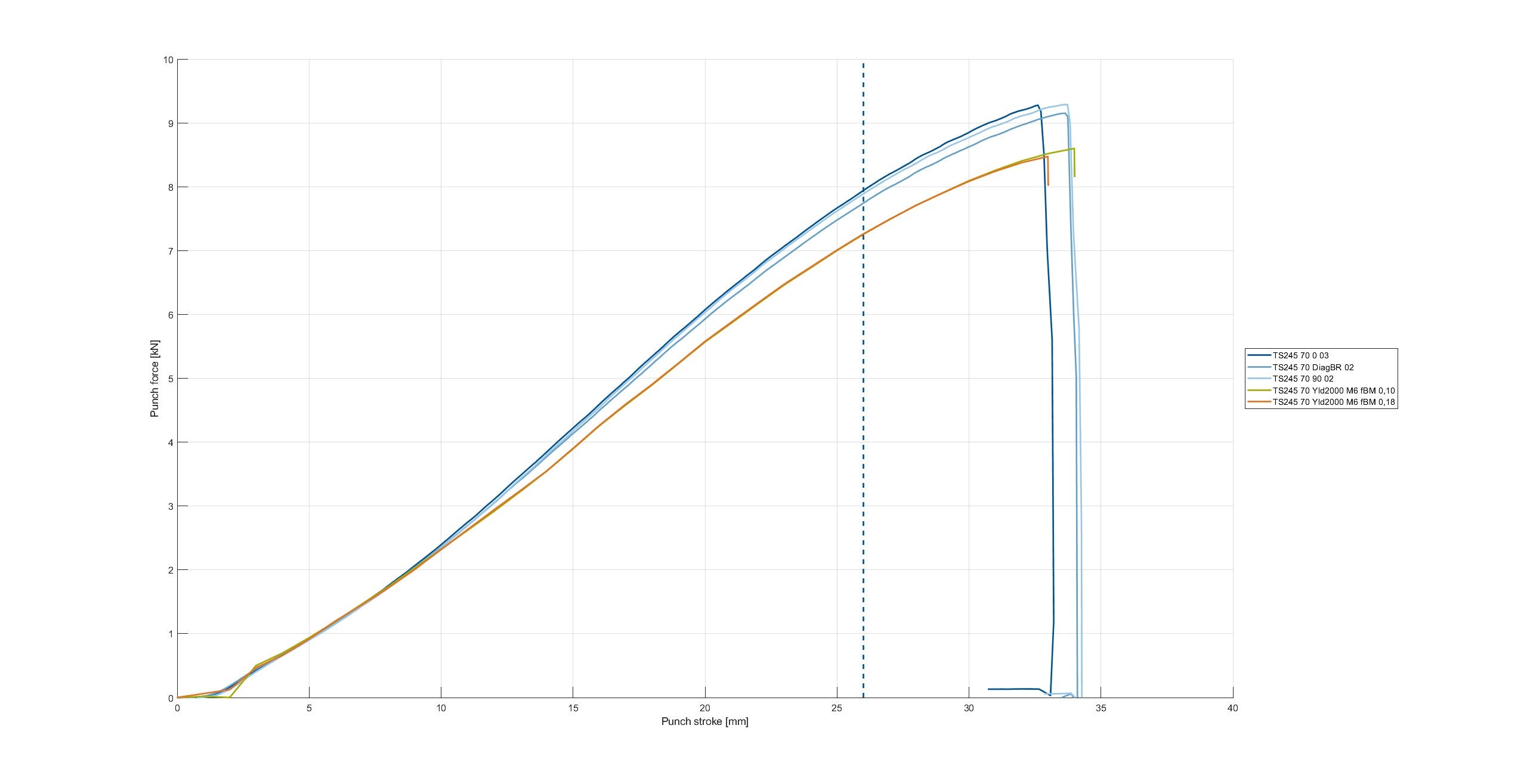
Thanks a lot for answering my question. For now I made a small changes in the yield curve and we can already see a huge improvement, now i want to know can i make it better by changing the Sigma bulge value ?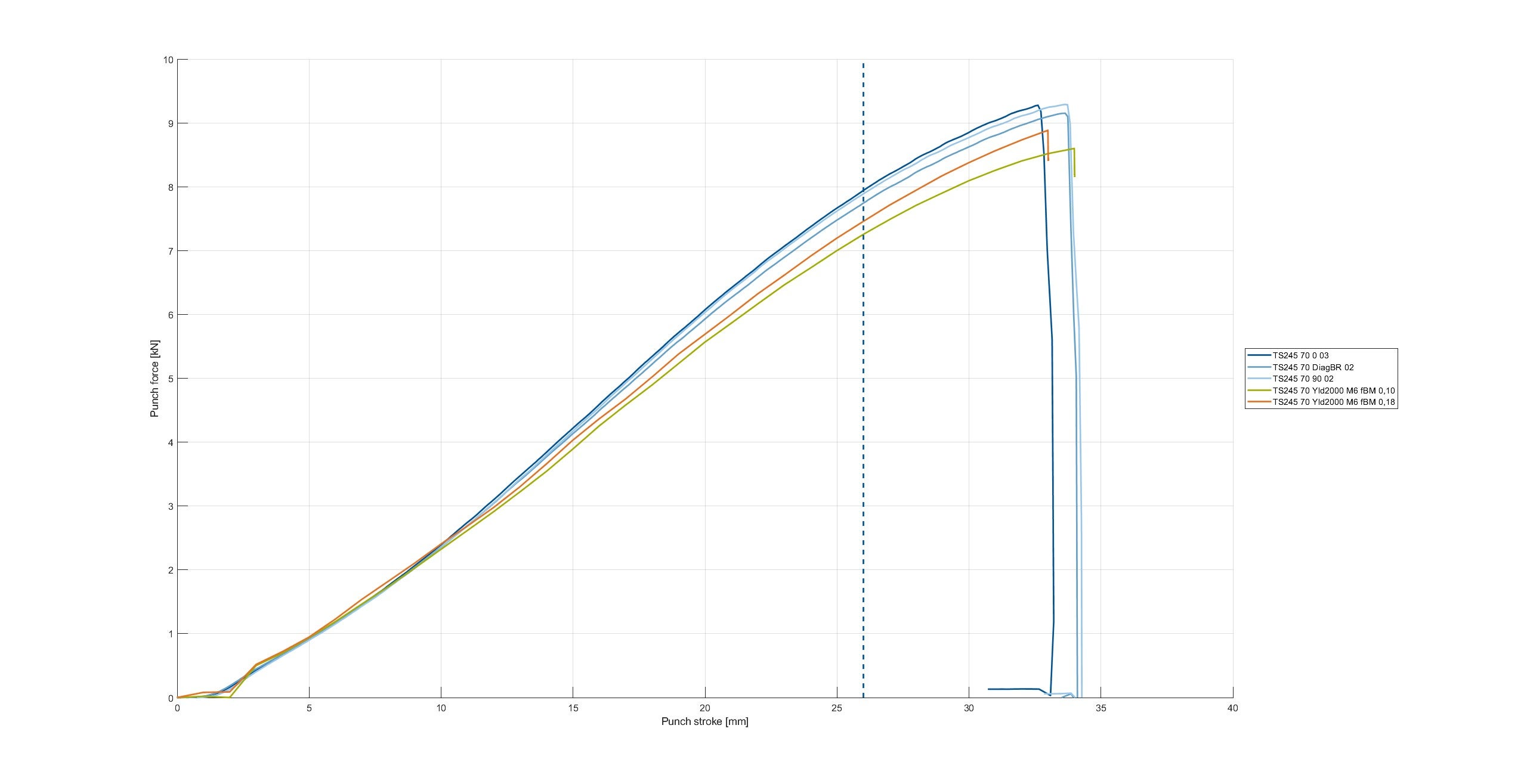 

 

The Orange curve is the new one. and the Green one is the old one. 
Best regards 

[Armin]

Hi Tarek,

I can see that your results have significantly improved. Although you may already have acceptable results, you can try adjusting the sigma bulge value in the calibration of the Yld2000 model to further enhance the predictions. You might consider calibrating it to a larger sb biaxial value. For example, if the initial yield occurs at sb = 1.05 but later the yield locus evolves such that sb = 1.10 might be a better representation, you can try recalibrating with sb = 1.10 to see how the predictions look like.